| > | read `/home/ph/maple/RC.txt`:read "/home/ph/maple/cartan.txt";unprotect(gamma); |
Warning, the name GramSchmidt has been rebound
Warning, the name GramSchmidt has been rebound
Warning, the name fibonacci has been rebound
Warning, `S1` is implicitly declared local to procedure `read2`
Warning, `CK` is implicitly declared local to procedure `read2`
Warning, `sp1` is implicitly declared local to procedure `read2`
Warning, `sn1` is implicitly declared local to procedure `read2`
Warning, `s1` is implicitly declared local to procedure `read2`
Warning, the names GramSchmidt and fibonacci have been rebound
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | with(PolynomialTools): |
Warning, the name MinimalPolynomial has been rebound
| > | read `/home/ph/maple/Solv.txt`; |
Warning, the names GramSchmidt and MinimalPolynomial have been rebound
![]()
| > | unassign('w'); |
| > | R:=transmat([3,4,4,6,6,2]):B:=transmat([2,1,5,3,1,5]): #rank 6; 32-41-45-63-61-25 STAR-CHECKED -- |
| > | R:=transmat([3,3,5,5,1,1]):B:=transmat([4,4,6,6,2,2]): #rank 6; PERIODIC |
| > | R:=transmat([5,5,5,1,1,1]):B:=transmat([3,3,4,6,2,2]): #rank 6; EXAMPLE ONE |
| > | R:=transmat([5,5,5,1,1,1]):B:=transmat([3,3,6,2,4,4]): #rank 6; EXAMPLE TWO |
| > | R:=transmat([3,4,5,5,1,1]):B:=transmat([2,3,6,6,4,2]): #rank 6;-- gamma 331/2048 |
| > | R:=transmat([3,4,5,6,1,2]):B:=transmat([2,3,6,5,4,1]): #rank 6; |
| > | R:=transmat([12,12,10,10,8,8,6,6,4,4,2,1]):B:=transmat([11,11,5,9,9,7,5,2,7,1,8,3]): #*************** 12 ************ |
| > | R:=transmat([12,12,1,2,4,1,5,5,1,2,1,1]):B:=transmat([7,11,8,3,9,10,6,6,10,9,9,10]): #rank 9; CHECKED |
| > | R:=transmat([4,4,4,7,7,7,1,1,1]):B:=transmat([2,9,5,8,3,8,5,6,2]): #rank 9; 42-49-45-78-73-78-15-16-12 *** NINER *** |
| > | R:=transmat([2,7,8,2,4,8,6,6]):B:=transmat([3,1,1,3,3,1,5,5]): #rank 5; 23-71-81-23-43-81-65-65 |
| > | R:=transmat([2,1,1,2,4,1,5,5]):B:=transmat([3,7,8,3,3,8,6,6]): #rank 5; 23-17-18-23-43-18-56-56 *******8********** |
| > | R:=transmat([2,3,2,5,4,5]):B:=transmat([5,4,6,2,1,3]): #rank 5 25-34-26-52-41-53 |
| > | R:=transmat([2,3,1,5,6,4]):B:=transmat([3,1,4,1,2,3]): #rank 5; 23-31-14-51-62-43 |
| > | R:=transmat([3,5,5,1,7,8,8,7]):B:=transmat([4,6,2,5,6,1,5,6]): #rank 6; ## CHECKED |
| > | R:=transmat([2,1,1,6,4,8,5,5]):B:=transmat([6,7,8,2,3,1,4,7]): #rank 6; 26-17-18-62-43-81-54-57 CHECKED |
| > | R:=transmat([2,1,1,2,4,1,5,5]):B:=transmat([3,7,8,3,3,8,6,6]): #rank 5; |
| > | R:=transmat([3,3,5,5,7,7,1,1]):B:=transmat([2,4,4,6,6,8,8,2]): # 32-34-54-56-76-78-18-12 CHECKED ***************************8************** |
| > | R:=transmat([3,3,5,6,7,7,1,2]):B:=transmat([2,4,4,5,6,8,8,1]): # 32-34-54-56-76-78-18-12 CHECKED |
| > | R:=transmat([2,4,4,2,6,5]):B:=transmat([3,6,5,3,1,4]):#rank 4 / CC 23-46-45-23-61-54 **************** 6 244265-365314 ***************** |
| > | R:=transmat([3,3,6,2,2,2]):B:=transmat([5,5,4,5,1,1]):#rank 4 & CC |
| > | R:=transmat([6,2,4,2,3,5]):B:=transmat([4,5,1,1,5,2]): #rank 5 / CC |
| > | R:=transmat([6,1,5,6,1,5]):B:=transmat([2,5,1,2,3,4]): #rank 5 / CC 62-15-51-62-13-54 --- checked for Delta |
| > | R:=transmat([2,3,1,3]):B:=transmat([4,4,2,2]): #rank 3, A invertible 24-34-12-32 --- checked for Delta ************ 2313-4422 ************ |
| > | R:=transmat([2,3,2,3]):B:=transmat([4,4,1,1]):#rank 3 &CC 24-34-21-31 --- checked for Delta same as 3311-2442 with 3<->4 |
| > | R:=transmat([4,3,1,2]):B:=transmat([3,4,4,3]):#rank 3 / CC 43-34-14-23 --- checked for Delta *****************************4********** |
| > | R:=transmat([3,3,1,1]):B:=transmat([2,4,4,2]):#rank 3 / CC 32-34-14-12 --- checked for Delta ******************** 3311-2442 ************ |
| > | R:=transmat([2,6,4,2,6,4]):B:=transmat([5,5,1,1,3,3]): # 25-65-41-21-63-43 --- checked for Delta |
| > | R:=transmat([4,4,1,1,7,7,3,4]):B:=transmat([5,6,2,2,8,8,2,6]): #rank 5 & CC CHECKED |
| > | R:=transmat([5,4,2,2,3]):B:=transmat([3,3,1,5,4]): #rank 4 / CC |
| > | R:=transmat([5,3,1,5,3,1]):B:=transmat([6,4,2,6,4,2]): #rank 3 / CC 56-34-12-56-34-12 --- checked for Delta |
| > | R:=transmat([5,4,4,2,6,5]):B:=transmat([3,6,5,3,1,4]): |
| > | R:=transmat([5,5,1,6,3,3]):B:=transmat([4,4,6,1,2,2]):# rank 3 54-54-16-61-32-32 --- checked for Delta *************6******************* |
| > | R:=transmat([2,3,2,2,3]):B:=transmat([1,4,1,5,4]): |
| > | R:=transmat([4,5,1,6,3,2]):B:=transmat([5,4,6,1,2,3]):# rank 3 |
| > | R:=transmat([3,3,5,5,1,2]):B:=transmat([4,4,6,6,2,3]):# rank 3 |
| > | R:=transmat([3,3,5,5,1,1]):B:=transmat([2,4,4,6,6,2]):# 32-34-54-56-16-12 |
| > | R:=transmat([3,4,6,5,1,2]):B:=transmat([4,3,5,6,2,3]):# 34-43-65-56-12-23 |
| > | R:=transmat([4,6,6,3,3,1,2]):B:=transmat([5,7,7,5,4,2,1]): |
| > | R:=transmat([3,4,5,5,1]):B:=transmat([2,3,1,1,4]): #rank 4 / CC 32-43-51-51-14 |
| > | R:=transmat([3,4,1,5,4]):B:=transmat([2,3,5,1,1]): #rank 4 / CC |
| > | R:=transmat([6,1,5,6,3,4]):B:=transmat([2,5,1,2,1,5]): |
| > | R:=transmat([6,1,5,6,1,5]):B:=transmat([2,5,1,2,3,4]): |
| > | R:=transmat([2,1,4,3,1]):B:=transmat([4,3,5,5,2]): |
| > | R:=transmat([3,3,5,5,1,1]):B:=transmat([2,4,6,6,4,2]): #rank 6; |
| > | R:=transmat([6,1,5,2,3,4]):B:=transmat([2,5,1,6,1,5]): #rank 6; R and B method does not work for this |
| > | R:=transmat([2,4,2,3]):B:=transmat([4,3,1,1]): |
| > | R:=transmat([2,1,2,2]):B:=transmat([3,3,4,3]): |
| > | R:=transmat([3,3,1,2]):B:=transmat([4,4,4,3]):#******************* renormalized 4312 3443 ****************** |
| > | R:=transmat([5,4,1,6,3,3]):B:=transmat([4,5,6,1,2,2]): |
| > | R:=transmat([5,5,1,6,3,2]):B:=transmat([4,4,6,1,2,3]): |
| > | R:=transmat([3,3,5,5,1,1,7,7]):B:=transmat([4,4,6,6,2,2,8,8]):#PERIODIC |
| > | R:=transmat([4,5,6,1,2,3]):B:=transmat([3,2,1,6,5,4]): # PERIODIC |
| > | R:=transmat([2,3,4,5,6,7,8,9,1]):B:=transmat([5,6,7,8,6,7,8,9,1]): # |
| > | R:=transmat([2,3,1]):B:=transmat([3,1,2]): |
| > | R:=transmat([3,3,1,1]):B:=transmat([4,4,2,2]): # PERIODIC |
| > | ############ START HERE ###################### |
| > | Delta:=evalm((R-B)/2):A:=evalm((R+B)/2): `R`=matrans(R);`B`=matrans(B); |
![]()
![]()
| > | unassign('e','a','w'):pi:=evalm(1/w[1]*linsolve(J-transpose(A),vector(n,0),'r',w));d:=rank(Delta):`rank of Delta`=d,`for n equals`=n;`rank of A`=rank(A);NA:=NullSpace(Matrix(A)):NTA:=NullSpace(Matrix(transpose(A))):nu:=nullity(Delta):zeta:=vector(n,0):u=vector(n,1):print("Delta",evalm(R-B)); |
| > | "A-CHECK",evalm(A^8),evalm(A^9),"trace-check",trace(A);liecliff(n):NN:=binomial(n,2):J2:=evalm(IdentityMatrix(NN)):uu:=vector(NN,1):unassign('e','x'):e:=vector(n):ee:=vector(n,1):ee:=evalm(e):phi:=diag(seq(ee[q],q=1..n)):psi:=sympow(phi,2): |
| > | R2:=sympow(R,2):B2:=sympow(B,2):#abel(R),abel(B),abel(R2),abel(B2),abel(A); |
| > | apart:=ecliffe(evalm(symult(A,J)+symult(Delta,J)));x:=vector(NN):Y:=matvec(x):ydet:=collect(trace(multiply(Y/2,apart)),[seq(x[k],k=1..n)]); |
| > | ISX:=NullSpace(Matrix(transpose(evalm(Delta)))):ND:=NullSpace(Matrix(Delta)): |
| > | CA:=r->if r>0 then concat(seq(NA[q],q=1..r)) else "" fi:CTA:=r->if r>0 then concat(seq(NTA[q],q=1..r)) else "" fi: |
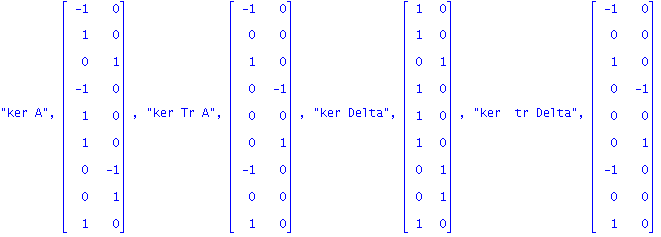
| > | "ker A",CA(nullity(A)),"ker Tr A",CTA(nullity(A)),"ker Delta",concat(seq(ND[q],q=1..nullity(Delta))),"ker tr Delta",concat(seq(ISX[q],q=1..nullity(Delta))); |
| > | P:=concat(seq(ND[q],q=1..nu),seq(zeta,q=1..d)):Q:=transpose(concat(seq(ISX[q],q=1..nu),seq(zeta,q=1..d))):Q:=submatrix(Q,1..n-d,1..n):print(Q);iszero(evalm(Delta&*P)),iszero(evalm(Q&*Delta));evalm(2*u&*Delta);"P",evalm(P); |
| > | `charpoly of A`=factor(collect(charpoly(A,s),s)):`rank of Delta`=rank(Delta);`charpoly of Delta`=factor(charpoly(Delta,s));`minpoly`=factor(minpoly(Delta,s));`invcharpoly`=collect(det(J-tau*Delta),tau):`d-th deriv of adjoint of id minus tau Delta`=row(map(diff,adjoint(J-tau*Delta),tau$d),1);ee:=vector(n,1):"rank of Omega union Delta"=rank(stackmatrix(pi,Delta)); |
PROCEDURES Sigma diag signs and MATADJ(mat,rownum) are here
| > | Sigma :=d-> matrix(d,d, (i,j)->if j=i then -(-1)^i else 0 fi): |
| > | MATADJ:=proc(mat,k) local i,nu,S:global x;nu:=rowdim(mat):x:=vector(nu):S:=Sigma(nu):for i to nu do x[i]:=ecliffit(Minor(Matrix(evalm(S&*(mat)&*S)),i,k)) od: evalm(x) end: |
| > | NATADJ:=proc(mat,k) local i,nu,S:global nx;nu:=rowdim(mat):nx:=vector(nu):S:=Sigma(nu):for i to nu do nx[i]:=ecliffit(Minor(Matrix(evalm(S&*(mat)&*S)),k,i)) od: evalm(nx) end: |
| > | sigma:=multiply(pi,u):spi:=evalm(pi/sigma);Omega:=stackmatrix(seq(spi,q=1..n)):#Hpi:=multiply(spi,F);Fpi:=multiply(spi,QD); |
J2 and AA are defined here also all ones JJ then PI and EI
| > | k:=2:NN:=binomial(n,2):J2:=evalm(IdentityMatrix(binomial(n,k))):AA:=evalm(sympow(A,2)):liecliff(n):JJ:=evalm(ConstantMatrix(1,n)): |
| > | #k:=3:print(seq({i,choose(n,k)[i]},i=1..binomial(n,k))); |
| > | LEVEL:=2:NL:=binomial(n,LEVEL):EI:=matrix(NL,n,0):for k to NL do va:=choose(n,LEVEL)[k];for i to LEVEL do EI[k,va[i]]:=1 od: od: |
| > | unassign('x'):q:=vector(NL):qq:=multiply(q,EI):vv:=linsolve(transpose(EI),spi,'r','x'); |
| > | z:=vector(NN):Z:=matvec(z):G:=multiply(Z,spi):PI:=jacobian(G,z): |
| > | Del2:=sympow(Delta,2):z2:=vector(NN,0):ND2:=nullspace(Del2):d2:=rank(Del2);P2:=concat(seq(ND2[k],k=1..nops(ND2)),seq(z2,j=1..d2)):"P2 available"; |
| > | z2:=vector(NN,0):nd2:=nullspace(transpose(Del2)):Q2:=stackmatrix(seq(nd2[k],k=1..nops(nd2)),seq(z2,j=1..d2)):"Q2 available"; |
![]()
![]()
![]()
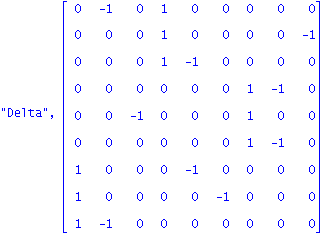

![apart := matrix([[1, 1/2, 1/2, 0, 0, 0, 0, 0, 1/2], [1/2, 1, 1/2, 0, 0, 0, 0, 0, 0], [1/2, 1/2, 1, 0, 0, 0, 1/2, 0, 0], [0, 0, 0, 1, 1/2, 1, 0, 0, 0], [0, 0, 0, 1/2, 1, 1/2, 0, 0, 0], [0, 0, 0, 1, 1/2...](images/RCCXX_28.gif)
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
AA is (numerical) Asup2. Use a2 for numerical A_2, j2a for numerical J2-AA
| > | A2:=evalm((1/2)*(R2+B2)):a2:=evalm(AA+Del2):iszero(A2-a2),"det",det(evalm(J2-AA)); |
![]()
| > | #print(sympow(R,2));print(sympow(B,2)); |
| > | j2a:=evalm(J2-AA):evalm(j2a),det(j2a),evalf(det(j2a)); |
| > | print("LEFT NULL",Q2,"DELTA2",Del2,"RIGHT NULL",P2);"DET",det(Del2); |
| > | rdd:=read2(Del2):for i to nops(rdd[1]) do print(convert(choose(n,2)[i],set),i,rdd[1][i]," ",rdd[2][i]) od; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
j2a2 is the numerical I-A_2
| > | j2a2:=evalm(j2a-Del2):"A_2",evalm(a2),"I-A_2",evalm(j2a2)," DET ",det(j2a2); |
| > | multiply((a2),uu); |
![]()
| > | unassign('x'):pi2:=evalm(1/x[1]*(linsolve(transpose(j2a2),vector(NN,0),'r',x)));u2:=evalm(1/x[1]*(linsolve(j2a2,vector(NN,0),'r',x))); |
![]()
![]()
OMEGA2 and E's coming up
| > | Omega2:=abel(a2);readcycles(Omega2); |
![Omega2 := matrix([[1/3, 0, 0, 0, 0, 2/3], [2/9, 0, 0, 0, 0, 4/9], [1/9, 0, 0, 0, 0, 2/9], [1/9, 0, 0, 0, 0, 2/9], [2/9, 0, 0, 0, 0, 4/9], [1/3, 0, 0, 0, 0, 2/3]])](images/RCCXX_93.gif)
![]()
| > | unassign('e','x'):e:=vector(n):ee:=vector(n,1):ee:=evalm(e):phi:=diag(seq(ee[q],q=1..n)):deta:=multiply(phi,Delta):psi:=sympow(phi,2): |
| > | APART:=ecliffe(evalm(symult(A,J)+symult(deta,J)));Y:=matvec(vv):ydt:=collect(trace(multiply(Y/2,APART)),[seq(x[k],k=1..n)]): |
| > | YDET:=add(x[k]*factor(diff(ydt,x[k])),k=1..2)+factor(subs([seq(x[k]=0,k=1..2)],ydt));D2:=sympow(deta,2): |
| > | A2:=evalm(AA+D2):"xA2",xtend(A2); |
![APART := matrix([[1, 1/2-1/2*e[1]*e[2], 1/4-1/4*e[1]*e[3], 1/4+1/4*e[1]*e[4]], [1/2-1/2*e[1]*e[2], 1, 1/4+1/4*e[2]*e[3], 1/4-1/4*e[2]*e[4]], [1/4-1/4*e[1]*e[3], 1/4+1/4*e[2]*e[3], 1, 0], [1/4+1/4*e[1]...](images/RCCXX_95.gif)
![]()
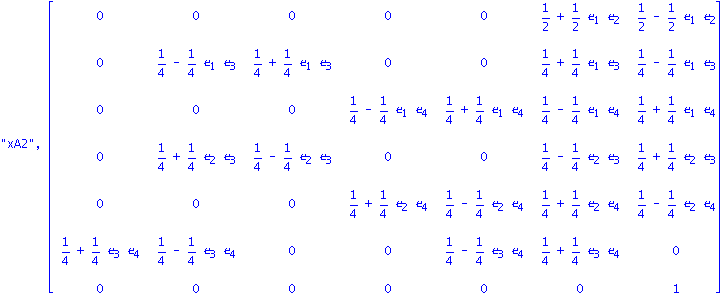
| > | J2A2:=evalm(J2-A2):evalm(J2A2); |
![matrix([[1, 0, 0, 0, 0, -1/2-1/2*e[1]*e[2]], [0, 3/4+1/4*e[1]*e[3], -1/4-1/4*e[1]*e[3], 0, 0, -1/4-1/4*e[1]*e[3]], [0, 0, 1, -1/4+1/4*e[1]*e[4], -1/4-1/4*e[1]*e[4], -1/4+1/4*e[1]*e[4]], [0, -1/4-1/4*e...](images/RCCXX_98.gif)
| > | det2:=det(J2A2):ud:=ecliffit(det2):"unis",ud,"gamma=",ecliffsubs(ud,zeta); |
![]()
DJ2 is the determinant with e's
| > | "FROM det Asup2",det(J2-AA);DJ2:=ud;gamma:=zcliffsubsmat(DJ2,vector(n,0)):"LOOKING FOR",gamma; |
![]()
![]()
![]()
| > | multiply(J2-AA,u2),multiply(Del2,u2),iszero(evalm(multiply(J2-AA,u2)-multiply(Del2,u2))); |
| > |
![]()
| > | V2:=multiply(Del2,inverse(J2-AA)); |
![V2 := matrix([[1/3, 1/2, 1/6, 1/6, 1/2, 4/3], [1/6, (-1)/16, 13/48, 7/48, 5/16, 2/3], [(-1)/6, (-5)/16, (-7)/48, (-13)/48, 1/16, (-2)/3], [(-1)/6, 1/16, (-13)/48, (-7)/48, (-5)/16, (-2)/3], [1/6, 5/16...](images/RCCXX_104.gif)
| > | beta:={4,5,6};dd:=ecliffit(goDET(beta,J2,V2)):cm:=evalm(cmat):dd,evalm(cmat);det(cmat); |
![]()
![7/96, matrix([[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [0, 0, 1, 0, 0, 0], [(-1)/6, 1/16, (-13)/48, (-7)/48, (-5)/16, (-2)/3], [1/6, 5/16, 7/48, 13/48, (-1)/16, 2/3], [1/3, (-1)/4, (-1)/12, (-1)/12, (-...](images/RCCXX_106.gif)
![]()
| > | "left",evalm(1/x[1]*linsolve(transpose(cmat),vector(NN,0),'r',x));"right",evalm(1/x[1]*linsolve(cmat,vector(NN,0),'r',x)); |
![]()
![]()
| > | #nu:=binomial(n,2):unassign('e','t','x','FX'):e:=vector(n):FX:=1:for i to nu do val:=choose(n,2)[i]:FX:=ecliffit(FX+FX*x[i]*e[val[1]]*e[val[2]]) |
| > | #od:G:=ecliffsubs(FX,vector(n,0)):nops(G); |
| > | #save(G,"/home/ph/maple/G"||n||".m"); |
| > | unassign('x'):read ("/home/ph/maple/G"||n||".m");#print(G); |
| > | gxc:=CORE(G,j2a,-Del2,true):print(gxc),"gamma",gamma; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | iszero(evalm(gxc[2])); |
![]()
| > | V2E:=multiply(psi,Del2,inverse(J2-AA)): |
| > | J2V2:=evalm(J2-V2E):ecliffit(det(J2V2)); |
![]()
| > | gvc:=CORE(G,J2,-V2,true):print(gvc,"CHECK",gvc[1]*det(j2a),"vs",gamma); |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | iszero(evalm(gxc[2]-gvc[2]*det(j2a))); |
![]()
| > | xrow:=MATADJ(J2-A2,1):ycol:=NATADJ(J2-A2,1): |
| > | X:=matvec(xrow):XY:=ecliffe(multiply(phi,X,phi)):Y:=matvec(ycol): |
| > | AJ:=ecliffe(adj(J2A2)): |
| > | AJBAR:=ecliffsubsmat(AJ,zeta);AJPBAR:=ecliffsubsmat(ecliffe(multiply(AJ,psi)),zeta); |
![AJBAR := matrix([[29/128, 11/128, 3/128, 3/128, 11/128, 1/4], [7/128, 21/64, 3/32, 1/16, 7/64, 1/4], [3/64, 15/128, 29/128, 13/128, 23/128, 1/4], [3/64, 23/128, 13/128, 29/128, 15/128, 1/4], [7/128, 7...](images/RCCXX_132.gif)
![AJPBAR := matrix([[5/128, (-3)/128, (-1)/128, (-1)/128, (-3)/128, 1/32], [3/128, (-3)/64, (-1)/16, (-1)/32, (-1)/64, (-1)/32], [1/64, 5/128, (-3)/128, (-3)/128, (-3)/128, (-1)/16], [1/64, (-3)/128, (-...](images/RCCXX_133.gif)
| > | evalm(multiply(AJBAR,J2-AA,P2)-multiply(AJPBAR,Del2,P2)),multiply(AJBAR,EI),multiply(PI,AJBAR); |
![matrix([[5/32, 5/32, 0, 0, 0, 0], [5/32, 0, 0, 0, 0, 0], [5/32, 0, 0, 0, 0, 0], [0, 5/32, 0, 0, 0, 0], [0, 5/32, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0]]), matrix([[43/128, 43/128, 23/64, 23/64], [61/128, 29/...](images/RCCXX_134.gif)
| > | XBAR:=ecliffsubsmat(X,zeta);XYBAR:=ecliffsubsmat(XY,zeta);YBAR:=ecliffsubsmat(Y,zeta);#YDELTABAR:=ecliffsubsmat(YDELTA,zeta); |
![XBAR := matrix([[0, 29/128, 11/128, 3/128], [29/128, 0, 3/128, 11/128], [11/128, 3/128, 0, 1/4], [3/128, 11/128, 1/4, 0]])](images/RCCXX_135.gif)
![XYBAR := matrix([[0, 5/128, (-3)/128, (-1)/128], [5/128, 0, (-1)/128, (-3)/128], [(-3)/128, (-1)/128, 0, 1/32], [(-1)/128, (-3)/128, 1/32, 0]])](images/RCCXX_136.gif)
![YBAR := matrix([[0, 29/128, 7/128, 3/64], [29/128, 0, 3/64, 7/128], [7/128, 3/64, 0, 17/128], [3/64, 7/128, 17/128, 0]])](images/RCCXX_137.gif)
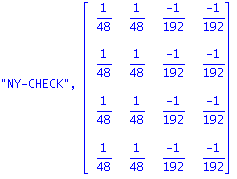
| > | "NY-CHECK",multiply(Omega,Delta,YBAR); |
| > | det(J2-AA),ecliffsubs(DJ2,zeta); |
![]()
| > | trace(multiply(XBAR,A,transpose(A)));trace(multiply(XYBAR,Delta,transpose(Delta)));"CHECK VAL",(1/2)*(%+%%); |
![]()
![]()
![]()
| > | multiply(u,XBAR,J-A); |
![]()
| > | multiply(xrow,EI):ecliffsubsmat(%,zeta); |
![]()
| > | ecliffe(evalm(multiply(XBAR-symmult(A,XBAR),P))); |
![matrix([[5/32, 0, 0, 0], [5/32, 0, 0, 0], [(-5)/32, 0, 0, 0], [(-5)/32, 0, 0, 0]])](images/RCCXX_145.gif)
| > | TR:=ecliffit(trace(evalm(X&*(A&*transpose(A)+deta&*transpose(deta))))); |
![]()
| > | nops(TR),ecliffsubs(TR,u); |
![]()
| > | TR-2*DJ2; |
![]()
| > | ecliffe(multiply(2*xrow,J2-A2)); |
![]()
| > | EIX:=multiply(xrow,EI):PIY:=multiply(PI,ycol): |
| > | EIXBAR:=ecliffsubsmat(EIX,zeta):PIYBAR:=ecliffsubsmat(PIY,zeta):print(EIXBAR,"vs",pi);print(PIYBAR,"vs",u); |
![]()
![]()
| > | unassign('x'):j2a2:=evalm(J2-(sympow(A,2)+sympow(Delta,2))):print(j2a2,"DET",det(j2a2)); |
![matrix([[1, 0, 0, 0, 0, -1], [0, 1, (-1)/2, 0, 0, (-1)/2], [0, 0, 1, 0, (-1)/2, 0], [0, (-1)/2, 0, 1, 0, 0], [0, 0, 0, (-1)/2, 1, (-1)/2], [(-1)/2, 0, 0, 0, 0, 1/2]]),](images/RCCXX_152.gif)
============ PI2 AND U2 CALCULATED HERE ==========================
| > | pi2:=evalm(1/x[1]*(linsolve(transpose(j2a2),vector(NN,0),'r',x)));u2:=evalm(1/x[1]*(linsolve(j2a2,vector(NN,0),'r',x))); |
![]()
![]()
| > | piV(pi2,2),"vs",evalm(pi);uV(u2,2),"vs",evalm(u); |
![]()
![]()
| > | V2:=multiply(Del2,inverse(J2-AA)):U2:=multiply(inverse(J2-AA),Del2):"DET",det(V2); |
![]()
| > | multiply(pi2,V2),"vs",evalm(pi2),multiply(U2,u2),"vs",evalm(u2); |
![]()
| > | v2e:=multiply(V2,EI):piu2:=multiply(PI,U2):print(v2e,piu2); |
![matrix([[1, 1, 2, 2], [3/8, 5/8, 3/4, 5/4], [(-5)/8, (-3)/8, (-5)/4, (-3)/4], [(-3)/8, (-5)/8, (-3)/4, (-5)/4], [5/8, 3/8, 5/4, 3/4], [0, 0, 0, 0]]), matrix([[5/18, (-31)/72, 11/72, (-1)/72, (-19)/72,...](images/RCCXX_159.gif)
| > | multiply(pi2,v2e),multiply(piu2,u2); |
![]()
| > | "Y-CHECK",subs([seq(y[k]=pi2[k],k=1..NN)],YDET); |
![]()
| > | Omega:=abel(A); |
![Omega := matrix([[1/6, 1/6, 1/3, 1/3], [1/6, 1/6, 1/3, 1/3], [1/6, 1/6, 1/3, 1/3], [1/6, 1/6, 1/3, 1/3]])](images/RCCXX_162.gif)
| > | unassign('e','tau'):e:=vector(n):phi:=diag(seq(e[i],i=1..n)): |
| > | factor(minpoly(R,s)),factor(minpoly(B,s));#JordanForm(Matrix(R),output=['J']),JordanForm(Matrix(B),output=['J']); |
![]()
| > | ###################### V CALCULATED HERE ################# |
| > | Eta:=evalm(J-(A-Omega)):EE:=evalm(Eta^(-1)):V:=evalm(Delta&*Eta^(-1)):print(V);N:=nullity(Delta): evalm(R&*EE),evalm(B&*EE); |
![matrix([[(-1)/6, 1/6, (-1)/3, 1/3], [1/6, (-1)/6, 1/3, (-1)/3], [1/2, (-1)/6, 0, (-1)/3], [(-1)/6, 1/2, (-1)/3, 0]])](images/RCCXX_164.gif)
![matrix([[(-1)/9, 2/9, 1/9, 7/9], [2/9, (-1)/9, 7/9, 1/9], [8/9, (-1)/9, 1/9, 1/9], [(-1)/9, 8/9, 1/9, 1/9]]), matrix([[2/9, (-1)/9, 7/9, 1/9], [(-1)/9, 2/9, 1/9, 7/9], [(-1)/9, 2/9, 1/9, 7/9], [2/9, (...](images/RCCXX_165.gif)
| > | ########################################################## |
| > | #UT(Matrix(R),Matrix(B)); |
| > | "n"=n;"rank Delta"=d;"pi"=evalm(pi);matrans(R),matrans(B);print(pi);OMEGA0:=row(adj(J-R),1);OMEGA1:=row(adj(J-B),1); |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | multiply(OMEGA0,J-V),multiply(OMEGA1,J+V),factor(charpoly(V,s));factor(charpoly(V2,s)); |
![]()
![]()
| > | ##################################################################################### |
| > | #################### !!!!!!!!!!!!!!!!!! START RUNS HERE !!!!!!!!!!!!! ###################################### |
| > | ##################################################################################### |
| > | print(matrans(R),matrans(B)); |
![]()
| > | "rank Delta"=rank(Delta);"rank A"=rank(A);"min-poly",factor(minpoly(Delta,x));unassign('phi','ee','e');print("pi",pi);liecliff(n); |
![]()
![]()
![]()
![]()
![]()
| > | d:=rank(Delta);n:=rowdim(A):zeta:=vector(n,0):ND:=nullspace(Delta);P:=concat(seq(ND[k],k=1..nops(ND)),seq(zeta,j=1..d)):nullspace(J-P); |
![]()
![]()
![]()
| > | print("YDET",YDET); |
![]()
DETTA DEFINED HERE
| > | ee:=[1,-1,1,1, -1, 1, 1,-1,1, 1, 1, 1]:phi:=diag(seq(ee[q],q=1..n)):Detta:=evalm(phi&*Delta):R:=evalm(A+Detta):B:=evalm(A-Detta):matrans(R),matrans(B);factor(minpoly(R,s)),factor(minpoly(B,s));nullspace(transpose(Detta));minpoly(Detta,x),factor(minpoly(Detta,x));D2:=sympow(Detta,2):psi:=sympow(phi,2): |
![]()
![]()
![]()
![]()
| > | "MORPHISM CHECK",iszero(evalm(psi&*Del2-D2)); |
![]()
| > | #ecliffsubs(YDET,ee);print(vv);unassign('x'):x:=vector(NN):X:=matvec(x):(1/2)*trace(multiply(X,symult(A,J)+symult(Detta,J))); |
| > | k:=3:RR:=extpowf(R,k):BB:=extpowf(B,k):#iszero(RR-sympow(R,k)),iszero(BB-sympow(B,k)); |
| > | #print(RR);print(BB); |
| > | NN:=binomial(n,k):JK:=evalm(IdentityMatrix(NN)): |
| > | A2:=evalm((1/2)*(RR+BB)):#factor(charpoly(A2,s));det(JK-A2);#det(J2-AA); |
TOMBSTONE ANALYSIS
| > | xJ2A2:=evalm(xtend(JK)-xtend(A2)): |
| > | unassign('x'):pi2:=evalm(1/x[1]*linsolve(transpose(xJ2A2),vector(1+NN,0),'r',x)):u2:=evalm(1/x[1]*linsolve(xJ2A2,vector(1+NN,0),'r',x)):print("pi2",pi2);print("u2",u2); |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | #AJ:=adj(xJ2A2); |
| > | #xa2:=xtend(A2); |
| > | #alpha:=abel(xa2);#"xA2",evalm(xa2),"abelx",evalm(alpha),iszero(alpha^2-alpha); |
| > | #evalm(xa2^(8)); |
| > | #Omega2:=abel(A2):aj:=adj(J2-A2):dt:=det(J2-A2):"det",dt,"abel",evalm(Omega2); if (iszero(Omega2-aj)) then print("true") else print("adj",aj) fi; |
| > | LEVEL:=3:NL:=binomial(n,LEVEL):#EI:=matrix(NL,n,0):for kx to NL do va:=choose(n,LEVEL)[kx];for i to LEVEL do EI[kx,va[i]]:=1 od: od: |
| > | unassign('x'):pi||k:=evalm(1/x[1]*linsolve(JK-transpose(A2),vector(NN,0),'r',x)):u||k:=evalm(1/x[1]*linsolve(JK-A2,vector(NN,0),'r',x)):print("pi"||k,pi||k);print("u"||k,u||k); |
![]()
![]()
![]()
![]()
| > | print(seq({i,choose(n,k)[i]},i=1..binomial(n,k))); |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | r:=k:print(pi||k):pi||k,readcycles(transpose(convert(pi||r,matrix))); |
![]()
![]()
![]()
| > | print(u||r);u||r,readcycles(transpose(convert(u||r,matrix))); |
![]()
![]()
![]()
![]()
![]()
| > | for i from r-1 to 1 by -1 do pi||i:=piV(pi||(i+1),i+1);u||i:=uV(u||(i+1),i+1) od; |
![]()
![]()
![]()
![]()
![]()
| > | unassign('y'):y:=vector(NN):Y:=matvec(y):z:=vector(NN):Z:=matvec(z):F:=multiply(u,Y):G:=multiply(Z,spi):PI:=jacobian(G,z):E:=transpose(jacobian(F,y)): |
| > | multiply(PI,u2),"vs u",evalm(u);multiply(pi2,E),"vs pi",evalm(pi); |
![]()
![]()
| > | rowdim(convert(pi2,matrix)); |
![]()
| > | M:=matvec(pi2):NX:=matvec(u2):N:=NX: |
| > | print("M",M,"N",NX); |
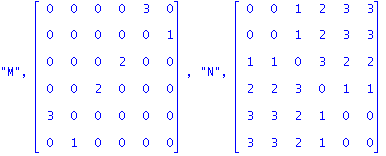
| > | "N-CHECK",evalm(Omega&*Detta&*NX);"PI-U CHECK",multiply(u,M)/multiply(u,M,u),evalm(pi),multiply(spi,NX)/multiply(spi,NX,spi); |
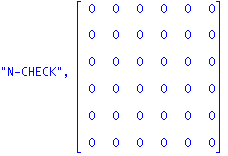
![]()
| > | NM:=evalm(NX&*M):MN:=evalm(M&*NX):scale:=add(NM[1,j],j=1..n);NM:=evalm(NM/scale):print("NM",NM,"MN",MN),"OMEGA-CHECKS",cmm(NM,Omega),"ABEL NM",abel(NM),"vs OMEGA",evalm(Omega); |
![]()
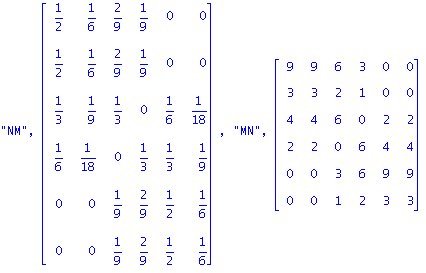
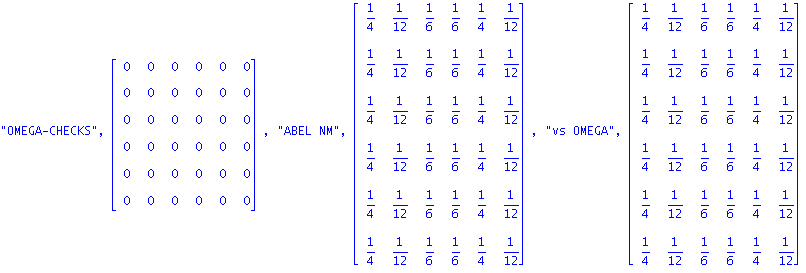
| > | RNB:=evalm( 1/2*(multiply(R,N,transpose(B))+multiply(B,N,transpose(R)))):evalm(N&*transpose(Omega)),evalm(RNB),evalm(N),multiply(RNB,transpose(Omega)); |
![matrix([[3/2, 3/2, 3/2, 3/2, 3/2, 3/2], [3/2, 3/2, 3/2, 3/2, 3/2, 3/2], [3/2, 3/2, 3/2, 3/2, 3/2, 3/2], [3/2, 3/2, 3/2, 3/2, 3/2, 3/2], [3/2, 3/2, 3/2, 3/2, 3/2, 3/2], [3/2, 3/2, 3/2, 3/2, 3/2, 3/2]])...](images/RCCXX_237.gif)
| > | "OMEGA",evalm(Omega),"PI-D-PI",multiply(transpose(Omega),Omega); |
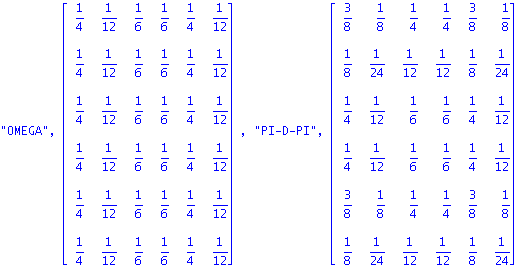
| > | "MCHECK PI-D-PI",multiply(M,Omega),"MCHK OMEGA",multiply(JJ,M),"NCHECK JJ",multiply(Omega,NX); |
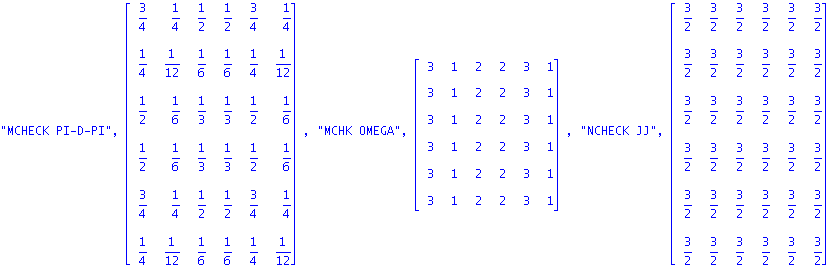
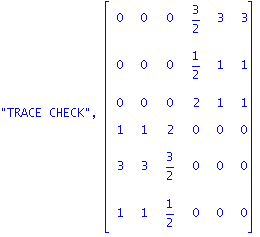
| > | "TRACE CHECK",evalm(M&*(symult(A,J)+symult(Detta,J))); |
| > | iszero(symmult(R,M)+symmult(B,M)-2*M),iszero(symult(A,NX)+symult(Detta,NX)-NX); |
![]()
| > | map(Re,map(evalf,Eigenvalues(Matrix(M)))),map(Re,map(evalf,Eigenvalues(Matrix(NX)))); |
, Vector[column]([[0.], [0.], [0.], [9.], [-2.438447187], [-6.561552813]])](images/RCCXX_242.gif)
| > | #checkspan(KBAS,NX),expVec(KBAS,NX); |
| > | adj(J-R); |
![matrix([[1, 0, 0, 0, 1, 0], [1, 0, 0, 0, 1, 0], [1, 0, 0, 0, 1, 0], [1, 0, 0, 0, 1, 0], [1, 0, 0, 0, 1, 0], [1, 0, 0, 0, 1, 0]])](images/RCCXX_243.gif)
| > | e:=vector(n):rterm:={}:v:=evalm(multiply(e,R)):for i to n do if (v[i]=0) then rterm:=rterm union {i} fi od:bterm:={}:v:=evalm(multiply(e,B)):for i to n do if (v[i]=0) then bterm:=bterm union {i} fi od:print("terminal points of R",rterm,"terminal points of B",bterm); |
| > | RCYC:=map(limit,evalm((1-s)*inverse(J-s*R)),s=1):BCYC:=map(limit,evalm((1-s)*inverse(J-s*B)),s=1): |
| > | unassign('S0','T0','s0','t0');RC:={}:S0:={}:s0:={}:k:=0:for IX to n do for i to n do if(RCYC[IX,i]<>0) then k:=k+1;s0:={i}union s0 fi; od;S0:=S0 union {s0};RC:=RC union s0;s0:={}: od:BC:={}:j:=0:T0:={}:t0:={}:for IX to n do for i to n do if(BCYC[IX,i]<>0) then j:=j+1;t0:={i} union t0 fi; od;T0:=T0 union {t0};BC:=BC union t0;t0:={} od:rcyc:=k*RCYC:bcyc:=evalm(j*BCYC):print("cycles in R",S0,"cycles in B",T0); |
| > | for i to n do if iszero(evalm((R^2)^i-R^i)) then print ("order of R is",i);break fi od;N:=i: |
| > | vv:=multiply(Delta,R^N,e):P0:={}:for i to n do if vv[i]=0 then P0:=P0 union {i} fi od: print("periodic points",P0);print("PN points",P0 minus RC); |
| > | for i to n do if iszero(evalm((B^2)^i-B^i)) then print ("order of B is",i);break fi od;N:=i: |
| > | vv:=multiply(Delta,B^N,e):Q0:={}:for i to n do if vv[i]=0 then Q0:=Q0 union {i} fi od: print("periodic points",Q0);print("PN points",Q0 minus BC); |
| > | antR:=(rterm minus RC) minus P0;antB:=(bterm minus BC) minus Q0; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | Y0[0]:=row(Omega,1):for i from 1 to d do Y0[i]:=map(simplify,multiply(Y0[0],Detta^(i))) od:K0:=stackmatrix(Y0[0],seq(Y0[0]+Y0[b],b=1..d)): dd:=d+1:print(K0,rank(K0),"out of",dd);Y1[0]:=row(Omega,1):for i from 1 to d do Y1[i]:=map(simplify,multiply(Y1[i-1],Detta)) od:K1:=stackmatrix(Y1[0],seq(Y1[0]-Y1[b],b=1..d)): dd:=d+1:print(K1,rank(K1),"out of",dd);print(stackmatrix(seq(Y0[b],b=1..d))); |
![matrix([[1/4, 1/12, 1/6, 1/6, 1/4, 1/12], [1/2, 0, 0, 0, 1/2, 0], [1/4, 1/6, 1/12, 1/12, 1/4, 1/6], [1/4, 1/8, 1/8, 1/8, 1/4, 1/8], [1/4, 5/48, 7/48, 7/48, 1/4, 5/48]]), 3,](images/RCCXX_254.gif)
![matrix([[1/4, 1/12, 1/6, 1/6, 1/4, 1/12], [0, 1/6, 1/3, 1/3, 0, 1/6], [1/4, 0, 1/4, 1/4, 1/4, 0], [1/4, 1/24, 5/24, 5/24, 1/4, 1/24], [1/4, 1/16, 3/16, 3/16, 1/4, 1/16]]), 3,](images/RCCXX_255.gif)
![matrix([[1/4, (-1)/12, (-1)/6, (-1)/6, 1/4, (-1)/12], [0, 1/12, (-1)/12, (-1)/12, 0, 1/12], [0, 1/24, (-1)/24, (-1)/24, 0, 1/24], [0, 1/48, (-1)/48, (-1)/48, 0, 1/48]])](images/RCCXX_256.gif)
| > | charpoly(Detta,t);factor(%); |
![]()
![]()
| > | map(simplify,multiply(spi,inverse(Matrix(evalm(J-t*Detta))))); |
![]()
| > | factor(1/simplify(det(J-t*Detta))); |
![]()
| > | KK:=stackmatrix(seq(Y0[b],b=1..d)); |
![KK := matrix([[1/4, (-1)/12, (-1)/6, (-1)/6, 1/4, (-1)/12], [0, 1/12, (-1)/12, (-1)/12, 0, 1/12], [0, 1/24, (-1)/24, (-1)/24, 0, 1/24], [0, 1/48, (-1)/48, (-1)/48, 0, 1/48]])](images/RCCXX_261.gif)
| > | NK:=nullspace(transpose(KK));rank(Del2); |
![]()
![]()
| > | ee:=vector(n,1):psi:=evalm(DiagonalMatrix(Vector(ee))): |
| > | for k from 1 to n do psi[k,k]:=-ee[k];Detta0:=multiply(psi,Detta):KA:=evalm(J2-AA-sympow(Detta0,2)); print(k,rank(KA),det(KA));psi[k,k]:=ee[k]; od: |
![]()
![]()
![]()
![]()
![]()
![]()
| > | #for k from 1 to n do phi[k,k]:=-ee[k]; |
| > | #Resolvent:=map(simplify,multiply(spi,inverse(Matrix(evalm(J-t*Detta))))): |
| > | #print(k,Resolvent); |
| > | #phi[k,k]:=ee[k]; od: |
| > | "minpoly",minpoly(Detta,s),factor(minpoly(Detta,s)); |
![]()
| > | print(rank(KK),d); |
![]()
| > | unassign('SU','ST','PDEL'): |
| > | #if ( rank(KK)=d) then mm:=minpoly(Detta,s):NKN:=CoefficientList(mm,s):ddd:=degree(mm)+1 : |
| > | #p:=add(NKN[j]*s^(j-1),j=1..ddd):q:=add(abs(NKN[j])*t^(j-1),j=1..ddd):print(p,q); |
| > | #PP:=evalm(subs(s=Detta,p)):QQ:=evalm(subs(t=A,q)):SA:=evalm(PP+QQ):rowsum:=multiply(SA,vector(n,1)):ST:=evalm(SA/rowsum[1]):SB:=evalm(-PP+QQ):rowsum:=multiply(SB,vector(n,1)):SU:=map(simplify,evalm(SB/rowsum[1])):print(PP,QQ,ST,SU,"cmm check",cmm(ST,Omega),cmm(SU,Omega));print( map(limit,evalm((1-s)*inverse(evalm(J-s*ST))),s=1),map(limit,evalm((1-s)*inverse(evalm(J-s*SU))),s=1)); fi: |
| > | if(rank(KK)<d) then for i to nullity(K0) do NKN:=[0,seq(NK[i][k],k=1..d)]; |
| > | p:=simplify(add(NKN[j]*s^(j-1),j=1..dd)):q:=simplify(add(abs(NKN[j])*t^(j-1),j=1..dd)):print(p,q); |
| > | PP:=evalm(subs(s=Detta,p)):PDEL[i]:=evalm(PP):QQ:=evalm(subs(t=A,q)):SA:=evalm(PP+QQ):rowsum:=multiply(SA,vector(n,1)):ST[i]:=map(simplify,evalm(SA/rowsum[1])):SB:=evalm(-PP+QQ):rowsum:=multiply(SB,vector(n,1)):SU[i]:=map(simplify,evalm(SB/rowsum[1])):print(PP,QQ,ST[i],SU[i],"cmm-check",cmm(ST[i],Omega),cmm(SU[i],Omega));print( map(limit,evalm((1-s)*inverse(evalm(J-s*ST[i]))),s=1),map(limit,evalm((1-s)*inverse(evalm(J-s*SU[i]))),s=1)); AST[i]:=evalm((1/2)*(ST[i]+SU[i]));print("AST",AST[i],"abel",abel(AST[i]), det(ST[i]),det(SU[i])) od;fi; |
![]()
![]()
Warning, computation interrupted
| > | unassign('x'):for k from 1 to 6 do nk:=binomial(n,k):jj:=evalm(IdentityMatrix(binomial(n,k))): R||k:=sympow(R,k):B||k:=sympow(B,k):A||k:=evalm((1/2)*(R||k+B||k)):pi||k:=evalm(1/x[1]*(linsolve(transpose(jj-A||k),vector(nk,0),'r',x)));u||k:=evalm(1/x[1]*(linsolve(jj-A||k,vector(nk,0),'r',x)));print(k,"","pi"||k,pi||k,"\n","u"||k,u||k," \n and ",piV(pi||k,k),"\n",uV(u||k,k)) od: |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | r:=4: #RANK |
| > | k:=r:print(seq({i,choose(n,k)[i]},i=1..binomial(n,k))); |
![]()
![]()
![]()
| > | readcycles(transpose(convert(pi||r,matrix))); |
![]()
| > | matrans(R),matrans(B); |
![]()
| > | print(u||r);readcycles(transpose(convert(u||r,matrix))); |
![]()
![]()
| > | for i from r-1 to 1 by -1 do pi||i:=piV(pi||(i+1),i+1);u||i:=uV(u||(i+1),i+1) od; |
![]()
![]()
![]()
![]()
![]()
![]()
| > | ########################################## RUNS ############################### |
TEMPLATE HERE
| > | #ee:=vector(n,1):for k from 0 to n do for i in choose(n,k) do ee:=vector(n,1): if (1 in i) then next fi;for j to n do if(j in i) then ee[j]:=-1 fi od; phi:=diag(seq(ee[q],q=1..n)); XXXXXXXXXXXXXXXXXXXXXXXXXX od;od; |
| > | #xu2:=evalm(1/x[1]*(linsolve(xjj,vector(1+NN,0),'r',x))); |
| > | ee:=vector(n,1):for k from 0 to n do for i in choose(n,k) do ee:=vector(n,1): if (1 in i) then next fi;for j to n do if(j in i) then ee[j]:=-1 fi od;phi:=diag(seq(ee[q],q=1..n));psi:=sympow(phi,2): jj:=(evalm(J2-AA-multiply(psi,Del2)));xjj:=(evalm(xtend(J2)-xtend(evalm(AA+multiply(psi,Del2)))));dj:=det(jj): if(dj=0) then print(ee);pi2:=evalm(1/x[1]*(linsolve(transpose(jj),vector(NN,0),'r',x)));u2:=evalm(1/x[1]*(linsolve(jj,vector(NN,0),'r',x))); print("pi2",pi2);print(readcycles(transpose(convert(pi2,matrix))));print("u2",u2); fi od;od; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | nl:=nullity(Delta); |
| > | #ee:=vector(n,1):unassign('x'):for k from 0 to n do for i in choose(n,k) do ee:=vector(n,1): if (1 in i) then next fi;for j to n do if(j in i) then ee[j]:=-1 fi od;phi:=diag(seq(ee[q],q=1..n));psi:=sympow(phi,2):d2:=multiply(psi,Del2): jj:=evalm(J2-AA-d2);xjj:=evalm(xtend(J2)-xtend(evalm(AA+d2)));pi2:=evalm(1/x[1]*(linsolve(transpose(jj),vector(NN,0),'r',x)));u2:=evalm(1/x[1]*(linsolve(jj,vector(NN,0),'r',x))); xu2:=evalm((linsolve(xjj,vector(1+NN,0),'r',x)));print(ee,"pi2",pi2,"u2",u2,"xu2",xu2);print(evalm(AA+d2),xtend(evalm(AA+d2))) od;od; |
| > | ########################################################################### |
| > | ################################### KERNEL ################################# |
| > | ########################################################################### |
| > | matrans(R),matrans(B); |
![]()
| > | unassign('IDEMS'):read "/home/ph/GAP/idems": |
| > | for i to doDIM(IDEMS) do matrans(IDEMS[i]),readcycles(IDEMS[i]) od; |
![]()
![]()
![]()
![]()
![]()
![]()
| > | for i in [1,2,3,4] do s[i]:=matrans(evalm(R^i)) od; |
![]()
![]()
![]()
![]()
| > | for i in [1,2] do s[i+4]:=matrans(evalm(B^i)) od; |
![]()
![]()
| > | for i in [1,2,3,4] do matrans(evalm(R^i&*B)) od; |
![]()
![]()
![]()
![]()
| > | for i in [1,2,3,4] do matrans(evalm(B^2&*R^i)) od; |
![]()
![]()
![]()
![]()
| > | unassign('ELSG'):read "/home/ph/GAP/elsg":for i to doDIM(ELSG) do matrans(evalm(ELSG[i])) od; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | C:=choose(n,2):print(seq({i,C[i]},i=1..binomial(n,2))); |
![]()
![]()
| > | #unassign('KROSPS','KRISPS'):print(Omega2); |
| > | #for i to doDIM(IDEMS) do KRISPS[i]:=multiply(evalm(IDEMS[i]),Omega):KROSPS[i]:=multiply(Omega,evalm(IDEMS[i])):print(KROSPS[i],KRISPS[i]) od: |
| > | #for i to doDIM(IDEMS) do checkspan(KBAS,IDEMS[i]) od; |
| > | #uu:=matrix(n,1,1): |
| > | #KRSPS:=stackmatrix(seq(KROSPS[i],i=1..doDIM(IDEMS))):RS:=rowspace(KRSPS);for i to doDIM(RS) do VS[i]:=evalm(uu&*transpose(convert(RS[i],matrix))) od; |
| > | #checkspan(VS,Omega),expVec(VS,Omega); |
| > | doDIM(IDEMS); |
| > | #MK:=stackmatrix(seq(KROSPS[i],i=1..doDIM(IDEMS)));rank(MK); |
| > | print(seq({k,choose(n,3)[k]},k=1..binomial(n,3))); |
| > | unassign('Q'):read "/home/ph/GAP/Q":for i to doDIM(Q) do matrans(evalm(Q[i])) od; |
![]()
![]()
![]()
![]()
| > | unassign('KBAS'):read "/home/ph/GAP/kbas":for i to doDIM(KBAS) do evalm(KBAS[i]) od:seq(evalm(KBAS[i]),i=1..doDIM(KBAS)); |
| > | #NNX:=subs([x[1]=1,x[2]=2],evalm(NX)); |
| > | checkspan(KBAS,NX);expVec(KBAS,NX);checkspan(KBAS,Omega);expVec(KBAS,Omega); |
| > | print(spi),p;ppr:=expand(p/s);evalm(PP-subs(s=Detta,p)); |
| > | PPR:=evalm(subs(s=Detta,ppr));checkspan(KBAS,PPR);expVec(KBAS,PPR); |
| > | checkspan(KBAS,Delta^2); |
| > | c:=4;MLT:=evalm(IDEMS[c]):doDIM(PDEL); |
| > | for i to doDIM(PDEL) do checkspan(KBAS,PDEL[i]) od;for i to doDIM(PDEL) do i,evalm(PDEL[i]),checkspan(KBAS,multiply(MLT,PDEL[i],MLT)) od; |
| > | #for i to doDIM(Q) do extpow(Q[i],2) od; |
| > | #for i to doDIM(IDEMS) do checkspan(KBAS,IDEMS[i]);expVec(KBAS,IDEMS[i]) od; |
| > | evalm(AA);evalm(a2-AA); |
![matrix([[0, 0, 0, 0, 0, 1/2], [0, 1/4, 1/4, 0, 0, 1/4], [0, 0, 0, 1/4, 1/4, 1/4], [0, 1/4, 1/4, 0, 0, 1/4], [0, 0, 0, 1/4, 1/4, 1/4], [1/4, 1/4, 0, 0, 1/4, 1/4]])](images/RCCXX_374.gif)
![matrix([[0, 0, 0, 0, 0, 1/2], [0, (-1)/4, 1/4, 0, 0, 1/4], [0, 0, 0, (-1)/4, 1/4, (-1)/4], [0, 1/4, (-1)/4, 0, 0, (-1)/4], [0, 0, 0, 1/4, (-1)/4, 1/4], [1/4, (-1)/4, 0, 0, (-1)/4, 1/4]])](images/RCCXX_375.gif)
| > | AAA:=sympow(A,3); |
![AAA := matrix([[0, 0, 1/4, 0], [0, 0, 0, 1/4], [1/8, 1/8, 1/8, 1/8], [1/8, 1/8, 1/8, 1/8]])](images/RCCXX_376.gif)
| > | a3:=evalm((1/2)*( sympow(R,3)+sympow(B,3)));del3:=evalm(AAA-a3); |
| > |
![a3 := matrix([[0, 0, 1/2, 0], [0, 0, 0, 1/2], [0, 1/2, 0, 0], [1/2, 0, 0, 0]])](images/RCCXX_377.gif)
![del3 := matrix([[0, 0, (-1)/4, 0], [0, 0, 0, (-1)/4], [1/8, (-3)/8, 1/8, 1/8], [(-3)/8, 1/8, 1/8, 1/8]])](images/RCCXX_378.gif)
| > | print(u2);xa2:=xtend(a2);xu2:=evalm((linsolve(xtend(J2)-xa2,vector(1+NN,0),'r',x))); |
![]()
![xa2 := matrix([[0, 0, 0, 0, 0, 1, 0], [0, 0, 1/2, 0, 0, 1/2, 0], [0, 0, 0, 0, 1/2, 0, 1/2], [0, 1/2, 0, 0, 0, 0, 1/2], [0, 0, 0, 1/2, 0, 1/2, 0], [1/2, 0, 0, 0, 0, 1/2, 0], [0, 0, 0, 0, 0, 0, 1]])](images/RCCXX_380.gif)
![]()
| > | evalm(a2),evalm(a2&*u2); |
![matrix([[0, 0, 0, 0, 0, 1], [0, 0, 1/2, 0, 0, 1/2], [0, 0, 0, 0, 1/2, 0], [0, 1/2, 0, 0, 0, 0], [0, 0, 0, 1/2, 0, 1/2], [1/2, 0, 0, 0, 0, 1/2]]), vector([3, 2, 1, 1, 2, 3])](images/RCCXX_382.gif)
| > | abel(a2); |
![matrix([[1/3, 0, 0, 0, 0, 2/3], [2/9, 0, 0, 0, 0, 4/9], [1/9, 0, 0, 0, 0, 2/9], [1/9, 0, 0, 0, 0, 2/9], [2/9, 0, 0, 0, 0, 4/9], [1/3, 0, 0, 0, 0, 2/3]])](images/RCCXX_383.gif)
| > | AN:=multiply(symult(A,N),transpose(Omega)); |
![AN := matrix([[3/2, 3/2, 3/2, 3/2, 3/2, 3/2], [3/2, 3/2, 3/2, 3/2, 3/2, 3/2], [3/2, 3/2, 3/2, 3/2, 3/2, 3/2], [3/2, 3/2, 3/2, 3/2, 3/2, 3/2], [3/2, 3/2, 3/2, 3/2, 3/2, 3/2], [3/2, 3/2, 3/2, 3/2, 3/2, ...](images/RCCXX_384.gif)
| > | evalm(transpose(Omega)); |
![matrix([[1/12, 1/12, 1/12, 1/12, 1/12, 1/12], [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/4, 1/4, 1/4, 1/4, 1/4, 1/4], [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 1/6, 1/6, 1/6, 1/6, ...](images/RCCXX_385.gif)
| > |
| > |