RCC.mw
| > |
read `/home/ph/maple/RC.txt`: |
Warning, the name GramSchmidt has been rebound
Warning, the name fibonacci has been rebound
Warning, the name MinimalPolynomial has been rebound
| > |
read `/home/ph/maple/Solv.txt`; |
Warning, the name MinimalPolynomial has been rebound
| > |
R:=transmat([3,4,4,6,6,2]):B:=transmat([2,1,5,3,1,5]): #rank 6; 32-41-45-63-61-25 CHECKED |
| > |
R:=transmat([3,3,5,5,1,1]):B:=transmat([4,4,6,6,2,2]): #rank 6; |
| > |
R:=transmat([3,4,5,5,1,1]):B:=transmat([2,3,6,6,4,2]): #rank 6; |
| > |
R:=transmat([3,4,5,6,1,2]):B:=transmat([2,3,6,5,4,1]): #rank 6; |
| > |
R:=transmat([12,12,1,2,4,1,5,5,1,2,1,1]):B:=transmat([7,11,8,3,9,10,6,6,10,9,9,10]): #rank 9; CHECKED |
| > |
R:=transmat([4,4,4,7,7,7,1,1,1]):B:=transmat([2,9,5,8,3,8,5,6,2]): #rank 9; 42-49-45-78-73-78-15-16-12 |
| > |
R:=transmat([2,7,8,2,4,8,6,6]):B:=transmat([3,1,1,3,3,1,5,5]): #rank 5; 23-71-81-23-43-81-65-65 |
| > |
R:=transmat([2,1,1,2,4,1,5,5]):B:=transmat([3,7,8,3,3,8,6,6]): #rank 5; 23-17-18-23-43-18-56-56 *******8********** |
| > |
R:=transmat([2,3,2,5,4,5]):B:=transmat([5,4,6,2,1,3]): #rank 5 25-34-26-52-41-53 |
| > |
R:=transmat([2,3,1,5,6,4]):B:=transmat([3,1,4,1,2,3]): #rank 5; 23-31-14-51-62-43 |
| > |
R:=transmat([3,5,5,1,7,8,8,7]):B:=transmat([4,6,2,5,6,1,5,6]): #rank 6; ## CHECKED |
| > |
R:=transmat([2,1,1,6,4,8,5,5]):B:=transmat([6,7,8,2,3,1,4,7]): #rank 6; 26-17-18-62-43-81-54-57 CHECKED |
| > |
R:=transmat([2,1,1,2,4,1,5,5]):B:=transmat([3,7,8,3,3,8,6,6]): #rank 5; |
| > |
R:=transmat([3,3,5,5,7,7,1,1]):B:=transmat([2,4,4,6,6,8,8,2]): # 32-34-54-56-76-78-18-12 CHECKED |
| > |
R:=transmat([3,3,5,6,7,7,1,2]):B:=transmat([2,4,4,5,6,8,8,1]): # 32-34-54-56-76-78-18-12 CHECKED |
| > |
R:=transmat([2,4,4,2,6,5]):B:=transmat([3,6,5,3,1,4]):#rank 4 / CC 23-46-45-23-61-54 |
| > |
R:=transmat([3,3,6,2,2,2]):B:=transmat([5,5,4,5,1,1]):#rank 4 & CC |
| > |
R:=transmat([6,2,4,2,3,5]):B:=transmat([4,5,1,1,5,2]): #rank 5 / CC |
| > |
R:=transmat([6,1,5,6,1,5]):B:=transmat([2,5,1,2,3,4]): #rank 5 / CC 62-15-51-62-13-54 --- checked for Delta |
| > |
R:=transmat([2,3,1,3]):B:=transmat([4,4,2,2]): #rank 3, A invertible 24-34-12-32 --- checked for Delta |
| > |
R:=transmat([2,3,2,3]):B:=transmat([4,4,1,1]):#rank 3 &CC 24-34-21-31 --- checked for Delta |
| > |
R:=transmat([4,3,1,2]):B:=transmat([3,4,4,3]):#rank 3 / CC 43-34-14-23 --- checked for Delta *****************************4********** |
| > |
R:=transmat([3,3,1,1]):B:=transmat([2,4,4,2]):#rank 3 / CC 32-34-14-12 --- checked for Delta |
| > |
R:=transmat([2,6,4,2,6,4]):B:=transmat([5,5,1,1,3,3]): # 25-65-41-21-63-43 --- checked for Delta |
| > |
R:=transmat([4,4,1,1,7,7,3,4]):B:=transmat([5,6,2,2,8,8,2,6]): #rank 5 & CC CHECKED |
| > |
R:=transmat([5,4,2,2,3]):B:=transmat([3,3,1,5,4]): #rank 4 / CC |
| > |
R:=transmat([5,3,1,5,3,1]):B:=transmat([6,4,2,6,4,2]): #rank 3 / CC 56-34-12-56-34-12 --- checked for Delta |
| > |
R:=transmat([5,4,4,2,6,5]):B:=transmat([3,6,5,3,1,4]): |
| > |
R:=transmat([5,5,1,6,3,3]):B:=transmat([4,4,6,1,2,2]):# rank 3 54-54-16-61-32-32 --- checked for Delta *************6******************* |
| > |
R:=transmat([2,3,2,2,3]):B:=transmat([1,4,1,5,4]): |
| > |
R:=transmat([4,5,1,6,3,2]):B:=transmat([5,4,6,1,2,3]):# rank 3 |
| > |
R:=transmat([3,3,5,5,1,2]):B:=transmat([4,4,6,6,2,3]):# rank 3 |
| > |
R:=transmat([3,3,5,5,1,1]):B:=transmat([2,4,4,6,6,2]):# 32-34-54-56-16-12 |
| > |
R:=transmat([3,4,6,5,1,2]):B:=transmat([4,3,5,6,2,3]):# 34-43-65-56-12-23 |
| > |
R:=transmat([4,6,6,3,3,1,2]):B:=transmat([5,7,7,5,4,2,1]): |
| > |
R:=transmat([3,4,5,5,1]):B:=transmat([2,3,1,1,4]): #rank 4 / CC 32-43-51-51-14 |
| > |
R:=transmat([3,4,1,5,4]):B:=transmat([2,3,5,1,1]): #rank 4 / CC |
| > |
R:=transmat([6,1,5,6,3,4]):B:=transmat([2,5,1,2,1,5]): |
| > |
R:=transmat([6,1,5,6,1,5]):B:=transmat([2,5,1,2,3,4]): |
| > |
R:=transmat([2,1,4,3,1]):B:=transmat([4,3,5,5,2]): |
| > |
R:=transmat([3,3,5,5,1,1]):B:=transmat([2,4,6,6,4,2]): #rank 6; |
| > |
R:=transmat([6,1,5,2,3,4]):B:=transmat([2,5,1,6,1,5]): #rank 6; R and B method does not work for this |
| > |
R:=transmat([2,3,2,1]):B:=transmat([4,4,1,3]): |
| > |
R:=transmat([5,4,6,6,3,3]):B:=transmat([4,5,1,1,2,2]): |
| > |
R:=transmat([2, 7, 8, 2, 4, 8, 6, 6]):B:=transmat([3, 1, 1, 3, 3, 1, 5, 5]): #rank |
| > |
R:=transmat([2,3,4,5,6,7,8,9,1,3]):B:=transmat([3,4,5,3,10,8,5,7,10,1]): # |
| > |
############ START HERE ###################### |
| > |
Delta:=evalm((R-B)/2):A:=evalm((R+B)/2): `R`=matrans(R);`B`=matrans(B); |
| > |
unassign('e','a','w'):pi:=evalm(1/w[1]*linsolve(J-transpose(A),vector(n,0),'r',w));d:=rank(Delta):`rank of Delta`=d,`for n equals`=n;`rank of A`=rank(A);NA:=NullSpace(Matrix(A)):NTA:=NullSpace(Matrix(transpose(A))):DA:=evalm(Delta&*A):(Delta,DA):`RankCheck1`=is(0=1-n+rank(stackmatrix(Delta,DA)));nu2:=nullity(evalm(Delta^2));nu:=nullity(Delta);`RankCheck2`=is((nu2-nu)<2);zeta:=vector(n,0):u=vector(n,1):print(evalm(R-B)); |
![R = vector([4, 3, 1, 2])](images/RCC2OUT_2.gif)
![B = vector([3, 4, 4, 3])](images/RCC2OUT_3.gif)
![pi := vector([1, 1, 2, 2])](images/RCC2OUT_4.gif)
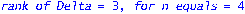
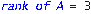
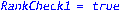
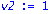
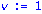
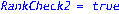
![matrix([[0, 0, -1, 1], [0, 0, 1, -1], [1, 0, 0, -1], [0, 1, -1, 0]])](images/RCC2OUT_11.gif)
| > |
k:=2:J2:=evalm(IdentityMatrix(binomial(n,k))):print(matrans(R),matrans(B)); |
![vector([4, 3, 1, 2]), vector([3, 4, 4, 3])](images/RCC2OUT_12.gif)
| > |
#Eigenvectors(Matrix(Delta)):TT:=map(fnormal,map(evalf,%[2]),4);factor(minpoly(Delta,x));map(abs,map(fnormal,multiply(pi,TT),3)); |
| > |
#FF:=FrobeniusForm(Matrix(Delta),output=['F','Q']);QD:=FF[2]:DQD:=FF[1]: |
| > |
#ED:=Eigenvalues(Matrix(Delta)):EDD:=map(fnormal,map(evalf,ED),3):print(EDD,map(fnormal,map(abs,EDD),3)); |
![matrix([[85/512, 85/512, 171/512, 171/512], [85/512, 85/512, 171/512, 171/512], [43/256, 85/512, 85/256, 171/512], [85/512, 43/256, 171/512, 85/256]]), 0](images/RCC2OUT_13.gif)
| > |
phi:=diag(seq(1,i=1..n)): |
| > |
phi[n,n]:=-1:detta:=multiply(phi,Delta): |
| > |
#Eigenvectors(Matrix(detta)):TT:=map(fnormal,map(evalf,%[2]),4); |
| > |
#for i to d do map(fnormal,multiply(A^i,TT),3);kol[i]:=col(%,2) od:stackmatrix(seq(kol[i],i=1..d));rank(%); |
| > |
unassign('tau');e:=vector(n):phi:=matrix(n,n,(i,j)->if i=j then e[i] else 0 fi): |
| > |
deta:=factor(det(A+tau*phi&*Delta)); |
![deta := -1/8*(1+tau*e[3])*(1+tau*e[4])*tau*(e[2]+e[1])](images/RCC2OUT_14.gif)
| > |
#ee:=[1,1,1,1,1,1,1,1]:#r:=ecliffsubsmat(evalm(A+phi&*Delta),ee);b:=ecliffsubsmat(evalm(A-phi&*Delta),ee);iszero(r+b-2*A); |
| > |
#factor(ecliffsubs(deta,ee)); |
| > |
ISX:=NullSpace(Matrix(transpose(evalm(Delta)))):ND:=NullSpace(Matrix(Delta)): |
| > |
CA:=r->if r>0 then concat(seq(NA[q],q=1..r)) else "" fi:CTA:=r->if r>0 then concat(seq(NTA[q],q=1..r)) else "" fi: |
| > |
"ker A",CA(nullity(A)),"ker Tr A",CTA(nullity(A)),"ker Delta",concat(seq(ND[q],q=1..nullity(Delta))),"ker tr Delta",concat(seq(ISX[q],q=1..nullity(Delta))); |

| > |
P:=concat(seq(ND[q],q=1..nu),seq(zeta,q=1..d)):Q:=transpose(concat(seq(ISX[q],q=1..nu),seq(zeta,q=1..d))):Q:=submatrix(Q,1..n-d,1..n):print(Q);iszero(evalm(Delta&*P)),iszero(evalm(Q&*Delta));evalm(2*u&*Delta); |
![matrix([[1, 1, 0, 0]])](images/RCC2OUT_16.gif)

![vector([1, 1, -1, -1])](images/RCC2OUT_18.gif)
| > |
`charpoly of A`=factor(collect(charpoly(A,s),s)):`rank of Delta`=rank(Delta);`charpoly of Delta`=factor(charpoly(Delta,s));`minpoly`=factor(minpoly(Delta,s));`invcharpoly`=collect(det(J-tau*Delta),tau):`d-th deriv of adjoint of id minus tau Delta`=row(map(diff,adjoint(J-tau*Delta),tau$d),1);ee:=vector(n,1):"rank of Omega union Delta"=rank(stackmatrix(pi,Delta)); |
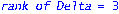
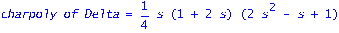
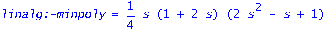
![`d-th deriv of adjoint of id minus tau Delta` = vector([3/4, 3/4, 0, 0])](images/RCC2OUT_22.gif)

| > |
sigma:=multiply(pi,u):spi:=evalm(pi/sigma);Omega:=stackmatrix(seq(spi,q=1..n)):#Hpi:=multiply(spi,F);Fpi:=multiply(spi,QD); |
![spi := vector([1/6, 1/6, 1/3, 1/3])](images/RCC2OUT_24.gif)
| > |
factor(minpoly(R,s)),factor(minpoly(B,s));#JordanForm(Matrix(R),output=['J']),JordanForm(Matrix(B),output=['J']); |
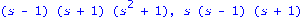
| > |
###################### V CALCULATED HERE ################# |
| > |
#Eta:=evalm(J-(A-Omega)):EE:=evalm(Eta^(-1)):V:=evalm(Delta&*Eta^(-1)):print(V);N:=nullity(Delta): |
| > |
########################################################## |
| > |
#UT(Matrix(R),Matrix(B)); |
| > |
#"n"=n;"rank Delta"=d;matrans(R),matrans(B);print(pi);OMEGA0:=row(adj(J-R),1);OMEGA1:=row(adj(J-B),1);VV:=multiply(Delta,inverse(J-B+adj(J-B))):VVV:=multiply(Delta,inverse(J-B+Omega)):zaz:=iszero(evalm((VV-VVV))); |
| > |
#for i to n do AX[i]:=evalm(extpowf(2*A,i)/(i+1)); LL[i]:=abel(AX[i]) od:print(seq(LL[i],i=1..n)); |
| > |
##################################################################### |
| > |
################################# MAIN RUN ############################ |
| > |
###################################################################### |
| > |
unassign('p','q','pp','qq'): |
| > |
e:=vector(n);phi:=diag(seq(e[q],q=1..n)):deta:=multiply(phi,Delta):#pp:=diag(seq(p[i],i=1..n)):qq:=diag(seq(q[i],i=1..n)): |
![e := array(1 .. 4, [])](images/RCC2OUT_26.gif)
| > |
RR:=evalm(A+deta):BB:=evalm(A-deta): |
| > |
k:=2:J2:=evalm(IdentityMatrix(binomial(n,k))): |
| > |
r:=evalm(sympow(RR,2)-J2):b:=evalm(sympow(BB,2)-J2):aj:=map(simplify,map(expand,evalm((r+b)))); |
![aj := matrix([[-2, 0, 0, 0, 0, 1+e[1]*e[2]], [0, -3/2-1/2*e[1]*e[3], 1/2+1/2*e[1]*e[3], 0, 0, 1/2+1/2*e[1]*e[3]], [0, 0, -2, 1/2-1/2*e[1]*e[4], 1/2+1/2*e[1]*e[4], 1/2-1/2*e[1]*e[4]], [0, 1/2+1/2*e[2]*...](images/RCC2OUT_27.gif)
| > |
#ecliffsubsmat(aj,[-1,1,-1,1,1,1,1,1]);det(%); |
| > |
#for i in [seq(e[j],j=1..n)] do trace(ecliffe(AD2&*map(diff,evalm(aj),i))) od; |
| > |
DD:=factor(simplify(ecliffit(det(aj)))); |
![DD := -1/4*tau^3*e[4]*e[1]-4*tau*e[3]*e[4]-5/4*tau^3*e[2]*e[4]-3/2*tau^2*e[2]*e[4]-1/4*e[3]*tau^3*e[4]*e[1]*e[2]-1/4*tau^3*e[3]*e[4]+1/2*tau^2*e[1]*e[4]+9/4*tau^2*e[3]*e[4]+3/4*tau*e[2]*e[4]+7/4*tau*e...](images/RCC2OUT_28.gif)
![DD := -1/4*tau^3*e[4]*e[1]-4*tau*e[3]*e[4]-5/4*tau^3*e[2]*e[4]-3/2*tau^2*e[2]*e[4]-1/4*e[3]*tau^3*e[4]*e[1]*e[2]-1/4*tau^3*e[3]*e[4]+1/2*tau^2*e[1]*e[4]+9/4*tau^2*e[3]*e[4]+3/4*tau*e[2]*e[4]+7/4*tau*e...](images/RCC2OUT_29.gif)
![DD := -1/4*tau^3*e[4]*e[1]-4*tau*e[3]*e[4]-5/4*tau^3*e[2]*e[4]-3/2*tau^2*e[2]*e[4]-1/4*e[3]*tau^3*e[4]*e[1]*e[2]-1/4*tau^3*e[3]*e[4]+1/2*tau^2*e[1]*e[4]+9/4*tau^2*e[3]*e[4]+3/4*tau*e[2]*e[4]+7/4*tau*e...](images/RCC2OUT_30.gif)
![12+(-1/4-1/4*e[1]*e[2])*tau^4+(-1/4*e[1]*e[4]-5/4*e[2]*e[4]-5/4*e[1]*e[3]-1/4*e[3]*e[4]*e[1]*e[2]-1/4*e[2]*e[3]-1/4*e[3]*e[4]+9/4*e[1]*e[2]-7/4)*tau^3+(1/2*e[1]*e[4]-23/4*e[3]*e[4]*e[1]*e[2]-3/2*e[1]*...](images/RCC2OUT_31.gif)
![12+(-1/4-1/4*e[1]*e[2])*tau^4+(-1/4*e[1]*e[4]-5/4*e[2]*e[4]-5/4*e[1]*e[3]-1/4*e[3]*e[4]*e[1]*e[2]-1/4*e[2]*e[3]-1/4*e[3]*e[4]+9/4*e[1]*e[2]-7/4)*tau^3+(1/2*e[1]*e[4]-23/4*e[3]*e[4]*e[1]*e[2]-3/2*e[1]*...](images/RCC2OUT_32.gif)
![12+(-1/4-1/4*e[1]*e[2])*tau^4+(-1/4*e[1]*e[4]-5/4*e[2]*e[4]-5/4*e[1]*e[3]-1/4*e[3]*e[4]*e[1]*e[2]-1/4*e[2]*e[3]-1/4*e[3]*e[4]+9/4*e[1]*e[2]-7/4)*tau^3+(1/2*e[1]*e[4]-23/4*e[3]*e[4]*e[1]*e[2]-3/2*e[1]*...](images/RCC2OUT_33.gif)
| > |
#collect(charpoly(aj,s),[s,tau]);factor(%); |
| > |
z:=grad(DD,e);#ecliffsubsmat(z,vector(n,1)); |
![z := vector([-1/4*tau^3*e[4]-1/4*tau^3*e[3]*e[4]*e[2]+1/2*tau^2*e[4]+7/4*tau*e[4]-23/4*tau^2*e[2]*e[3]*e[4]-3/2*tau^2*e[3]+3/4*tau*e[3]-5/4*tau^3*e[3]+9/4*tau^3*e[2]-4*tau*e[2]-1/4*tau^4*e[2], -5/4*ta...](images/RCC2OUT_34.gif)
![z := vector([-1/4*tau^3*e[4]-1/4*tau^3*e[3]*e[4]*e[2]+1/2*tau^2*e[4]+7/4*tau*e[4]-23/4*tau^2*e[2]*e[3]*e[4]-3/2*tau^2*e[3]+3/4*tau*e[3]-5/4*tau^3*e[3]+9/4*tau^3*e[2]-4*tau*e[2]-1/4*tau^4*e[2], -5/4*ta...](images/RCC2OUT_35.gif)
![z := vector([-1/4*tau^3*e[4]-1/4*tau^3*e[3]*e[4]*e[2]+1/2*tau^2*e[4]+7/4*tau*e[4]-23/4*tau^2*e[2]*e[3]*e[4]-3/2*tau^2*e[3]+3/4*tau*e[3]-5/4*tau^3*e[3]+9/4*tau^3*e[2]-4*tau*e[2]-1/4*tau^4*e[2], -5/4*ta...](images/RCC2OUT_36.gif)
![z := vector([-1/4*tau^3*e[4]-1/4*tau^3*e[3]*e[4]*e[2]+1/2*tau^2*e[4]+7/4*tau*e[4]-23/4*tau^2*e[2]*e[3]*e[4]-3/2*tau^2*e[3]+3/4*tau*e[3]-5/4*tau^3*e[3]+9/4*tau^3*e[2]-4*tau*e[2]-1/4*tau^4*e[2], -5/4*ta...](images/RCC2OUT_37.gif)
| > |
ecliffsubs(DD,[1,1,1,-1,1,1,1]); |
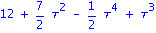
| > |
#unassign('Y','YY');Y[0]:=evalm(spi):for i from 1 to d do Y[i]:=map(simplify,multiply(Y[i-1],deta)) od:KU:=((stackmatrix(seq(spi+Y[b],b=0..d)))); |
| > |
#map(factor,ecliffe(sympow(KUU,2))); |
| > |
#KUU:=ecliffe(map(simplify,multiply(KU,transpose(KU)))); |
| > |
ee:=vector(n,1):print(ee),ecliffsubsmat(KUU,ee);det(%); |
![vector([1, 1, 1, 1])](images/RCC2OUT_39.gif)
![matrix([[10/9, 4/9, 11/18, 19/36], [4/9, 5/18, 7/36, 17/72], [11/18, 7/36, 13/36, 5/18], [19/36, 17/72, 5/18, 37/144]])](images/RCC2OUT_40.gif)

| > |
z:=factor(ecliffit(z1)); |
![z := 1/10368*e[4]*e[1]-11/93312*e[3]*e[1]*e[4]*e[2]-1/10368*e[4]*e[2]+7/93312*e[4]*e[3]-25/93312*e[1]*e[2]-1/10368*e[3]*e[1]+1/10368*e[3]*e[2]+29/93312](images/RCC2OUT_42.gif)
| > |
ZVal:=ecliffsubs(z1,vector(n,0));ifactor(%); |
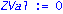

| > |
ZVal:=ecliffsubs(z,vector(n,0));ifactor(%); |
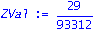
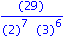
| > |
ee:=vector(n,1):ZVal:=ecliffsubs(z,ee);ee[2]:=-1:ee[6]:=1:ZVal:=ecliffsubs(z,ee); |
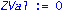
Error, 1st index, 6, larger than upper array bound 4
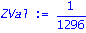
| > |
gZ:=grad(z,e):ecliffsubsmat(gZ,ee); |
![vector([1/2592, (-1)/2592, 0, 1/2592])](images/RCC2OUT_49.gif)
| > |
c:=8;ee[c]:=-ee[c]:print("ee=",ee);Zval:=ecliffsubs(z,ee); |
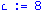
Error, 1st index, 8, larger than upper array bound 4
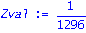
| > |
KK:=ecliffsubsmat(KUV,vector(n,1)); |
![KK := matrix([[10/9, 4/9, 11/18, 19/36], [4/9, 5/18, 7/36, 17/72], [11/18, 7/36, 13/36, 5/18], [19/36, 17/72, 5/18, 37/144]])](images/RCC2OUT_53.gif)
| > |
map(Re,map(evalf,Eigenvalues(Matrix(KK)))); |
](images/RCC2OUT_54.gif)
| > |
##################################################################################### |
| > |
#################### !!!!!!!!!!!!!!!!!! START RUNS HERE !!!!!!!!!!!!! ###################################### |
| > |
##################################################################################### |
| > |
print(matrans(R),matrans(B),submatrix(Q,1..n-d,1..n),pi); |
![vector([4, 3, 1, 2]), vector([3, 4, 4, 3]), matrix([[1, 1, 0, 0]]), vector([1, 1, 2, 2])](images/RCC2OUT_55.gif)
| > |
"rank Delta"=rank(Delta);"rank A"=rank(A);"min-poly",factor(minpoly(Delta,x));unassign('phi','ee');print("pi",pi); |


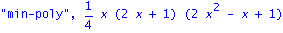
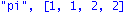
| > |
#OR:=multiply(Omega,R);OB:=multiply(Omega,B);checkspan(VS,OR),checkspan(VS,OB);expVec(VS,OR),expVec(VS,OB); |
| > |
########################## RANK RUNS ############################### |
| > |
d:=rank(Delta);n:=rowdim(A):zeta:=vector(n,0):ND:=nullspace(Delta);P:=concat(seq(ND[k],k=1..nops(ND)),seq(zeta,j=1..d)):nullspace(J-P); |
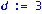
![ND := {vector([1, 1, 1, 1])}](images/RCC2OUT_61.gif)
![{vector([1, 1, 1, 1])}](images/RCC2OUT_62.gif)
| > |
ee:=[1,-1,1,-1,-1,-1,1,1,1,1]:phi:=diag(seq(ee[q],q=1..n)):Detta:=phi&*Delta:R:=evalm(A+Detta):B:=evalm(A-Detta):matrans(R),matrans(B);factor(minpoly(R,s)),factor(minpoly(B,s));nullspace(transpose(Detta));minpoly(Detta,x),factor(minpoly(Detta,x)); |
![vector([4, 4, 1, 3]), vector([3, 3, 4, 2])](images/RCC2OUT_63.gif)
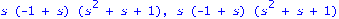
![{vector([-1, 1, 0, 0])}](images/RCC2OUT_65.gif)
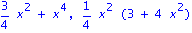
| > |
R:=evalm(RR):B:=evalm(BB): |
| > |
k:=3:RR:=extpowf(R,k):BB:=extpowf(B,k):print(RR,BB);iszero(RR-sympow(R,k)),iszero(BB-sympow(B,k)); |
![matrix([[0, 0, 1, 0], [0, 0, 0, 1], [0, 1, 0, 0], [1, 0, 0, 0]]), matrix([[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]])](images/RCC2OUT_67.gif)

| > |
print(seq({i,choose(n,k)[i]},i=1..binomial(n,k))); |
![{1, [1]}, {2, [2]}, {3, [3]}, {4, [4]}](images/RCC2OUT_69.gif)
| > |
AA:=evalm((1/2)*(RR+BB));extpow(A,k);#print(evalm(2*AA),abel(AA)); |
![AA := matrix([[0, 0, 1/2, 0], [0, 0, 0, 1/2], [0, 1/2, 0, 0], [1/2, 0, 0, 0]])](images/RCC2OUT_70.gif)
![matrix([[0, 0, 0, 0], [0, 0, 0, 0], [1/8, 1/8, 1/8, 1/8], [1/8, 1/8, 1/8, 1/8]])](images/RCC2OUT_71.gif)
| > |
matrans(asym2(R)),matrans(asym2(B)); |
![vector([trf[1], 3, 6, 3, 6, 2]), vector([trf[1], 6, 4, 6, 4, 5])](images/RCC2OUT_72.gif)
| > |
rterm:={}:v:=evalm(multiply(e,R)):for i to n do if (v[i]=0) then rterm:=rterm union {i} fi od:bterm:={}:v:=evalm(multiply(e,B)):for i to n do if (v[i]=0) then bterm:=bterm union {i} fi od:print("terminal points of R",rterm,"terminal points of B",bterm); |
| > |
RCYC:=map(limit,evalm((1-s)*inverse(J-s*R)),s=1):BCYC:=map(limit,evalm((1-s)*inverse(J-s*B)),s=1): |
| > |
unassign('S0','T0','s0','t0');RC:={}:S0:={}:s0:={}:k:=0:for IX to n do for i to n do if(RCYC[IX,i]<>0) then k:=k+1;s0:={i}union s0 fi; od;S0:=S0 union {s0};RC:=RC union s0;s0:={}: od:BC:={}:j:=0:T0:={}:t0:={}:for IX to n do for i to n do if(BCYC[IX,i]<>0) then j:=j+1;t0:={i} union t0 fi; od;T0:=T0 union {t0};BC:=BC union t0;t0:={} od:rcyc:=k*RCYC:bcyc:=evalm(j*BCYC):print("cycles in R",S0,"cycles in B",T0); |
| > |
for i to n do if iszero(evalm((R^2)^i-R^i)) then print ("order of R is",i);break fi od;N:=i: |
| > |
vv:=multiply(Delta,R^N,e):P0:={}:for i to n do if vv[i]=0 then P0:=P0 union {i} fi od: print("periodic points",P0);print("PN points",P0 minus RC); |
| > |
for i to n do if iszero(evalm((B^2)^i-B^i)) then print ("order of B is",i);break fi od;N:=i: |
| > |
vv:=multiply(Delta,B^N,e):Q0:={}:for i to n do if vv[i]=0 then Q0:=Q0 union {i} fi od: print("periodic points",Q0);print("PN points",Q0 minus BC); |
| > |
antR:=(rterm minus RC) minus P0;antB:=(bterm minus BC) minus Q0; |
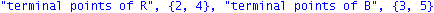
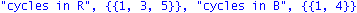

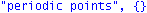


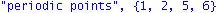
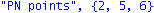

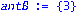
| > |
Y0[0]:=row(Omega,1):for i from 1 to d do Y0[i]:=map(simplify,multiply(Y0[0],Detta^(i))) od:K0:=stackmatrix(Y0[0],seq(Y0[0]+Y0[b],b=1..d)): dd:=d+1:print(K0,rank(K0),"out of",dd);Y1[0]:=row(Omega,1):for i from 1 to d do Y1[i]:=map(simplify,multiply(Y1[i-1],Detta)) od:K1:=stackmatrix(Y1[0],seq(Y1[0]-Y1[b],b=1..d)): dd:=d+1:print(K1,rank(K1),"out of",dd);print(stackmatrix(seq(Y0[b],b=1..d))); |
![matrix([[1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 0, 1/3, 0, 1/3, 1/6], [1/3, 1/12, 1/4, 1/4, 1/12, 0], [1/6, 7/24, 1/24, 1/8, 5/24, 1/6]]), 4,](images/RCC2OUT_83.gif)
![matrix([[1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 1/3, 0, 1/3, 0, 1/6], [0, 1/4, 1/12, 1/12, 1/4, 1/3], [1/6, 1/24, 7/24, 5/24, 1/8, 1/6]]), 4,](images/RCC2OUT_84.gif)
![matrix([[0, (-1)/6, 1/6, (-1)/6, 1/6, 0], [1/6, (-1)/12, 1/12, 1/12, (-1)/12, (-1)/6], [0, 1/8, (-1)/8, (-1)/24, 1/24, 0]])](images/RCC2OUT_85.gif)
| > |
charpoly(Detta,t);factor(%); |
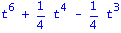
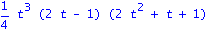
| > |
map(simplify,multiply(spi,inverse(Matrix(evalm(J-t*Detta))))); |
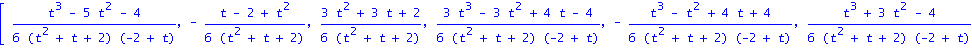

| > |
factor(1/simplify(det(J-t*Detta))); |
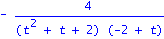
| > |
Series:=map(simplify,evalm(multiply(spi,add(evalm(psi[n]*Detta^n),n=0..d)))):Resolvent:=map(simplify,multiply(spi,inverse(Matrix(evalm(J-t*Detta))))):MM:=evalm(Series-Resolvent): |
| > |
sys:=solve({seq(MM[i],i=1..n)},{seq(psi[n],n=0..d)}); |
![sys := {psi[0] = 1, psi[1] = -t*(t^2+4)/(-4-t^2+t^3), psi[3] = -4*t^3/(-4-t^2+t^3), psi[2] = -4*t^2/(-4-t^2+t^3)}](images/RCC2OUT_91.gif)
| > |
KK:=stackmatrix(seq(Y0[b],b=1..d)); |
![KK := matrix([[0, (-1)/6, 1/6, (-1)/6, 1/6, 0], [1/6, (-1)/12, 1/12, 1/12, (-1)/12, (-1)/6], [0, 1/8, (-1)/8, (-1)/24, 1/24, 0]])](images/RCC2OUT_92.gif)
| > |
NK:=nullspace(transpose(KK)); |
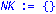
| > |
for k from 1 to n do phi[k,k]:=-ee[k]; Y0[0]:=Omega:for i from 1 to d do Y0[i]:=map(simplify,multiply(Y0[i-1],Detta)) od:KA[k]:=stackmatrix(seq(row(Y0[b],1),b=0..d)); print(k,rank(KA[k]));phi[k,k]:=ee[k]; od: |
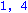
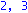
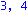
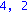
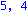
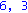
| > |
#for k from 1 to n do phi[k,k]:=-ee[k]; |
| > |
#Resolvent:=map(simplify,multiply(spi,inverse(Matrix(evalm(J-t*Detta))))): |
| > |
"minpoly",minpoly(Detta,s),factor(minpoly(Detta,s)); |
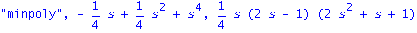
| > |
if ( rank(KK)=d) then mm:=minpoly(Detta,s):NKN:=CoefficientList(mm,s):ddd:=degree(mm)+1 : |
| > |
p:=add(NKN[j]*s^(j-1),j=1..ddd):q:=add(abs(NKN[j])*t^(j-1),j=1..ddd):print(p,q); |
| > |
PP:=evalm(subs(s=Detta,p)):QQ:=evalm(subs(t=A,q)):SA:=evalm(PP+QQ):rowsum:=multiply(SA,vector(n,1)):ST:=evalm(SA/rowsum[1]):SB:=evalm(-PP+QQ):rowsum:=multiply(SB,vector(n,1)):SU:=map(simplify,evalm(SB/rowsum[1])):print(PP,QQ,ST,SU,"cmm check",cmm(ST,Omega),cmm(SU,Omega));print( map(limit,evalm((1-s)*inverse(evalm(J-s*ST))),s=1),map(limit,evalm((1-s)*inverse(evalm(J-s*SU))),s=1)); fi: |
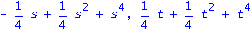
![matrix([[0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0]]), matrix([[1/4, 1/4, 1/4, 1/4, 1/4, 1/4], [1/4, 1/4, 1/4, 1/4, 1/4, 1/4]...](images/RCC2OUT_102.gif)
![matrix([[0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0]]), matrix([[1/4, 1/4, 1/4, 1/4, 1/4, 1/4], [1/4, 1/4, 1/4, 1/4, 1/4, 1/4]...](images/RCC2OUT_103.gif)
![matrix([[1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 1/6, 1/6, 1/6, 1/6, 1/6]])...](images/RCC2OUT_104.gif)
| > |
if(rank(KK)<d) then for i to nullity(K0) do NKN:=[0,seq(NK[i][k],k=1..d)]; |
| > |
p:=add(NKN[j]*s^(j-1),j=1..dd):q:=add(abs(NKN[j])*t^(j-1),j=1..dd):print(p,q); |
| > |
PP:=evalm(subs(s=Detta,p)):QQ:=evalm(subs(t=A,q)):SA:=evalm(PP+QQ):rowsum:=multiply(SA,vector(n,1)):ST:=map(simplify,evalm(SA/rowsum[1])):SB:=evalm(-PP+QQ):rowsum:=multiply(SB,vector(n,1)):SU:=map(simplify,evalm(SB/rowsum[1])):print(PP,QQ,ST,SU,"cmm-check",cmm(ST,Omega),cmm(SU,Omega));print( map(limit,evalm((1-s)*inverse(evalm(J-s*ST))),s=1),map(limit,evalm((1-s)*inverse(evalm(J-s*SU))),s=1)); print(checkspan(KBAS,SU),checkspan(KBAS,ST),expVec(KBAS,SU),expVec(KBAS,ST)) od;fi; |
| > |
ee:=[1,1,-1,-1,1,-1,-1,-1]:unassign('p','q'):for i to n do assume(0<p[i] and p[i]<1) od: |
| > |
k:=2:JJ:=IdentityMatrix(binomial(n,k)):phi:=diag(seq(ee[i],i=1..n)): Detta:=Matrix(multiply(phi,Delta)): |
| > |
RR:=extpowf(evalm(A+Detta),k):BB:=extpowf(evalm(A-Detta),k):AA:=evalm((1/2)*(RR+BB)):LL:=map(limit,evalm((1-s)*inverse(JJ-s*AA)),s=1): |
| > |
print(iszero(LL)," ",AA,LL); |

| > |
#checkspan(KBAS,SU),checkspan(KBAS,ST);expVec(KBAS,SU),expVec(KBAS,ST); |
| > |
#map(limit,evalm((1-s)*inverse(J-s*ST)),s=1),map(limit,evalm((1-s)*inverse(J-s*SU)),s=1); |
| > |
#JordanForm(Matrix(evalm(ST))),FrobeniusForm(Matrix(ST)),cmm(SA,Omega),det(SA); |
| > |
#JordanForm(Matrix(evalm(SU))),FrobeniusForm(Matrix(SU)),cmm(SB,Omega),det(SB); |
| > |
#for i to 26 do COC[i]:=map(diff,CO,h[i]) od:print(seq(COC[i],i=1..10));checkspan(COC,ST);expVec(COC,SA);COCC:=Centr(SA,Omega); |
| > |
#unassign('CX'):nx:=6;for i to nx do CX[i]:=map(diff,COCC,h[i]) od:print(seq(CX[k],k=1..doDIM(CX)),Omega); |
| > |
########################## RUNNING EIGHTS ############################### |
| > |
#for i1 in 1 do for i2 in 1,2 do for i3 in 1,2 do for i4 in 1,2 do for i5 in 1,2 do for i6 in 1,2 do for i7 in 1,2 do for i8 in 1,2 do |
| > |
#ee:=[bit[i1],bit[i2],bit[i3],bit[i4],bit[i5],bit[i6],bit[i7],bit[i8]];phi:=diag(seq(ee[q],q=1..n)); Detta:=Matrix(multiply(phi,Delta)); |
| > |
#RR:=asym2(evalm(A+Detta)):BB:=asym2(evalm(A-Detta));AA:=evalm((1/2)*(RR+BB)):LL:=map(limit,evalm((1-s)*inverse(JJ-s*AA)),s=1);print(ee,iszero(LL)); |
| > |
#od;od;od;od;od;od;od;od; |
| > |
####################### RUN NINE ############################## |
| > |
for i1 in 1 do for i2 in 1,2 do for i3 in 1,2 do for i4 in 1,2 do for i5 in 1,2 do for i6 in 1,2 do for i7 in 1,2 do for i8 in 1,2 do for i9 in 1,2 do ee:=[bit[i1],bit[i2],bit[i3],bit[i4],bit[i5],bit[i6],bit[i7],bit[i8],bit[i9]]; phi:=diag(seq(ee[q],q=1..n));unassign('Y');Y[1]:=multiply(Omega,phi,Delta):for i from 2 to d do Y[i]:=map(simplify,multiply(Y[i-1],phi,Delta)) od:KK:=stackmatrix(seq((row(Y[b],1),b=1..d)));eee:=evalm((1/2)*(ee+u));unassign('Y0','Y1');VV:=evalm(phi&*Delta&*inverse(J-A+Omega));RR:=evalm(A+phi&*Delta):BB:=evalm(A-phi&*Delta):OMEGA0:=evalm(pi&*adj(J-VV));OMEGA1:=evalm(pi&*adj(J+VV));d1:=rank(BB);d2:=rank(RR);Y0[0]:=OMEGA0:for i from 1 to d do Y0[i]:=map(simplify,multiply(Y0[i-1],phi,Delta)) od:K0:=stackmatrix(seq(Y0[b],b=1..d)); Y1[0]:=OMEGA1:for i from 1 to d do Y1[i]:=map(simplify,multiply(Y1[i-1],phi,Delta)) od:K1:=stackmatrix(seq(Y1[b],b=1..d));if (d=rank(K0) and d=rank(K1)) then RESULT:="IT WORKS" else RESULT:="check" fi; print(eee,evalb(d=rank(KK)),"rank RR ",d2,"rank K1 ",rank(K1),"rank BB ",d1,"rank K0 ",rank(K0), evalb(d=rank(K1))," ",evalb(d=rank(K0)),RESULT) od;od;od;od;od;od;od;od;od;#od;od;od; |
Error, invalid subscript selector
| > |
################################################# |
| > |
#for i1 in 1 do for i2 in 1,2 do for i3 in 1,2 do for i4 in 1,2 do for i5 in 1,2 do for i6 in 1,2 do ee:=[bit[i1],bit[i2],bit[i3],bit[i4],bit[i5],bit[i6]]; phi:=diag(seq(ee[q],q=1..n)); |
| > |
Detta:=Matrix(multiply(phi,Delta));R:=evalm(A+Detta):B:=evalm(A-Detta); print("R",matrans(R),"B",matrans(B));rterm:={}:v:=evalm(multiply(e,R)):for i to n do if (v[i]=0) then rterm:=rterm union {i} fi od:bterm:={}:v:=evalm(multiply(e,B)):for i to n do if (v[i]=0) then bterm:=bterm union {i} fi od:print("terminal points of R",rterm,"terminal points of B",bterm);RCYC:=map(limit,evalm((1-s)*inverse(J-s*R)),s=1):BCYC:=map(limit,evalm((1-s)*inverse(J-s*B)),s=1):unassign('S0','T0','s0','t0');RC:={}:S0:={}:s0:={}:k:=0:for IX to n do for i to n do if(RCYC[IX,i]<>0) then k:=k+1;s0:={i}union s0 fi; od;S0:=S0 union {s0};RC:=RC union s0;s0:={}: od:BC:={}:j:=0:T0:={}:t0:={}:for IX to n do for i to n do if(BCYC[IX,i]<>0) then j:=j+1;t0:={i} union t0 fi; od;T0:=T0 union {t0};BC:=BC union t0;t0:={} od:rcyc:=k*RCYC:bcyc:=evalm(j*BCYC):print("cycles in R",S0,"cycles in B",T0);for i to n do if iszero(evalm((R^2)^i-R^i)) then print ("order of R is",i);break fi od;N:=i:vv:=multiply(Delta,R^N,e):P0:={}:for i to n do if vv[i]=0 then P0:=P0 union {i} fi od: print("periodic points",P0);print("PN points",P0 minus RC);for i to n do if iszero(evalm((B^2)^i-B^i)) then print ("order of B is",i);break fi od;N:=i:vv:=multiply(Delta,B^N,e):Q0:={}:for i to n do if vv[i]=0 then Q0:=Q0 union {i} fi od: print("periodic points",Q0);print("PN points",Q0 minus BC);antR:=(rterm minus RC) minus P0;antB:=(bterm minus BC) minus Q0;print("ant R",antR,"ant B",antB);print("minpoly",minpoly(Detta,s)); |
| > |
Y0[0]:=Omega:for i from 1 to d do Y0[i]:=map(simplify,multiply(Y0[i-1],Detta)) od:K0:=stackmatrix(seq(row(Y0[b],1),b=1..d)): print(ee,rank(K0),K0);for k from 1 to n do phi[k,k]:=-ee[k]; Y0[0]:=Omega:for i from 1 to d do Y0[i]:=map(simplify,multiply(Y0[i-1],phi,Delta)) od:KA[k]:=stackmatrix(seq(row(Y0[b],1),b=1..d)); print(k,rank(KA[k]));phi[k,k]:=ee[k]; od: |
| > |
dd:=d+1:if(rank(K0)<d) then NK:=nullspace(transpose(K0));print("NullSpace",NK) ;for i to nullity(K0) do NKN:=[0,seq(NK[i][k],k=1..d)];p:=add(NKN[j]*s^(j-1),j=1..dd):q:=add(abs(NKN[j])*t^(j-1),j=1..dd):print(p,q);PP:=evalm(subs(s=Detta,p)):QQ:=evalm(subs(t=A,q)):SA:=evalm(PP+QQ):rowsum:=multiply(SA,vector(n,1)):ST:=evalm(SA/rowsum[1]):SB:=evalm(-PP+QQ):rowsum:=multiply(SB,vector(n,1)):SU:=map(simplify,evalm(SB/rowsum[1])):print(PP,QQ,ST,SU,"cmm",cmm(ST,SU),cmm(SU,Omega),cmm(ST,Omega));print( map(limit,evalm((1-s)*inverse(evalm(J-s*ST))),s=1),map(limit,evalm((1-s)*inverse(evalm(J-s*SU))),s=1));od; fi; |
| > |
if ( rank(K0)=d) then mm:=minpoly(Detta,s):NKN:=CoefficientList(mm,s);dd:=degree(mm)+1; |
| > |
p:=add(NKN[j]*s^(j-1),j=1..dd):q:=add(abs(NKN[j])*t^(j-1),j=1..dd):print(p,q); |
| > |
PP:=evalm(subs(s=Detta,p)):QQ:=evalm(subs(t=A,q)):SA:=evalm(PP+QQ):rowsum:=multiply(SA,vector(n,1)):ST:=evalm(SA/rowsum[1]):print(PP,QQ,ST);print(map(limit,evalm((1-s)*inverse(evalm(J-s*ST))),s=1));fi; print("=============================================") od;od;od;od;od;od; |
| > |
################################################################## |
| > |
############################## ANOTHER SIXES ############################# |
| > |
################################################################## |
| > |
mmm:=map(abs,map(fnormal,multiply(pi,TT),3)); |
| > |
#for i1 in 1 do for i2 in 1,2 do for i3 in 1,2 do for i4 in 1,2 do for i5 in 1,2 do for i6 in 1,2 do od;od;od;od;od;od; |
| > |
k:=2:J2:=IdentityMatrix(binomial(n,k)):print(matrans(R),matrans(B)); |
![vector([4, 5, 1, 6, 3, 2]), vector([5, 4, 6, 1, 2, 3])](images/RCC2OUT_106.gif)
| > |
print(seq({i,choose(n,k)[i]},i=1..binomial(n,k))); |
![{1, [1, 2]}, {2, [1, 3]}, {3, [1, 4]}, {4, [1, 5]}, {5, [1, 6]}, {6, [2, 3]}, {7, [2, 4]}, {8, [2, 5]}, {9, [2, 6]}, {10, [3, 4]}, {11, [3, 5]}, {12, [3, 6]}, {13, [4, 5]}, {14, [4, 6]}, {15, [5, 6]}](images/RCC2OUT_107.gif)
![{1, [1, 2]}, {2, [1, 3]}, {3, [1, 4]}, {4, [1, 5]}, {5, [1, 6]}, {6, [2, 3]}, {7, [2, 4]}, {8, [2, 5]}, {9, [2, 6]}, {10, [3, 4]}, {11, [3, 5]}, {12, [3, 6]}, {13, [4, 5]}, {14, [4, 6]}, {15, [5, 6]}](images/RCC2OUT_108.gif)
| > |
#for i1 in 1 do for i2 in 1,2 do for i3 in 1,2 do for i4 in 1,2 do for i5 in 1,2 do for i6 in 1,2 do ee:=[bit[i1],bit[i2],bit[i3],bit[i4],bit[i5],bit[i6]];phi:=diag(seq(ee[q],q=1..n)); Detta:=Matrix(multiply(phi,Delta)); |
| > |
#RR:=extpowf(evalm(A+Detta),k):BB:=extpowf(evalm(A-Detta),k);AA:=evalm((1/2)*(RR+BB)):LL:=map(limit,evalm((1-s)*inverse(J2-s*AA)),s=1);print(ee,iszero(LL),det(J2-AA)); |
![Matrix([[-.8880, .2950, .4813, 2.043], [.3157, .6855, -1.769, 1.102], [.4347, -2.196, -0.3228e-1, 1.074], [1., 1., 1., 1.]])](images/RCC2OUT_109.gif)
| > |
ee:=[1,1,1,1,1,1];phi:=diag(seq(ee[q],q=1..n)):deta:=multiply(phi,Delta): |
![ee := [1, 1, 1, 1, 1, 1]](images/RCC2OUT_110.gif)
| > |
PP:=map(simplify,multiply(Omega,deta,res(lambda,deta))):rank(deta); |

| > |
#NS:=NullSpace(Matrix(subs(lambda=0,evalm(map(diff,PP,lambda))))); |
| > |
#for i to nullity(PP) do multiply(Delta,NS[i]) od; |
| > |
##################### FOURS ###################### |
| > |
"rank Delta"=rank(Delta);matrans(R),matrans(B);print(pi);svd(Delta); |

![vector([4, 3, 1, 3]), vector([3, 4, 4, 2])](images/RCC2OUT_113.gif)
![vector([1, 1, 2, 2])](images/RCC2OUT_114.gif)
![matrix([[-.1954395076, -.5116672736, -.8278950396, .1207882584], [-.5116672736, -.1954395076, .1207882584, -.8278950396], [.8278950396, -.1207882584, -.1954395076, -.5116672736], [.1207882584, -.82789...](images/RCC2OUT_115.gif)
| > |
#print(map(get2,UU),map(get2,DD),map(get2,VT),map(get2,H),map(get2,K)); |
| > |
for i1 in 1 do for i2 in 1,2 do for i3 in 1,2 do for i4 in 1,2 do ee:=[bit[i1],bit[i2],bit[i3],bit[i4]];phi:=diag(seq(ee[q],q=1..n)); Detta:=Matrix(multiply(phi,Delta)); |
| > |
Y0[0]:=Omega:for i from 1 to d do Y0[i]:=map(simplify,multiply(Y0[i-1],Detta)) od:K0:=stackmatrix(seq(row(Y0[b],1),b=1..d)): print(ee,rank(K0),K0);for k from 1 to n do phi[k,k]:=-ee[k]; Y0[0]:=Omega:for i from 1 to d do Y0[i]:=map(simplify,multiply(Y0[i-1],phi,Delta)) od:KA[k]:=stackmatrix(seq(row(Y0[b],1),b=1..d)); print(k,rank(KA[k]));phi[k,k]:=ee[k]; od: |
| > |
dd:=d+1:if(rank(K0)<d) then NK:=nullspace(transpose(K0));print("NullSpace",NK) ;for i to nullity(K0) do NKN:=[0,seq(NK[i][k],k=1..d)];p:=add(NKN[j]*s^(j-1),j=1..dd):q:=add(abs(NKN[j])*t^(j-1),j=1..dd):print(p,q);PP:=evalm(subs(s=Detta,p)):QQ:=evalm(subs(t=A,q)):SA:=evalm(PP+QQ):rowsum:=multiply(SA,vector(n,1)):ST:=evalm(SA/rowsum[1]):print(PP,QQ,ST);od fi; |
| > |
if ( rank(K0)=d) then mm:=minpoly(Detta,s):NKN:=CoefficientList(mm,s);dd:=degree(mm)+1; |
| > |
p:=add(NKN[j]*s^(j-1),j=1..dd):q:=add(abs(NKN[j])*t^(j-1),j=1..dd):print(p,q); |
| > |
PP:=evalm(subs(s=Detta,p)):QQ:=evalm(subs(t=A,q)):SA:=evalm(PP+QQ):rowsum:=multiply(SA,vector(n,1)):ST:=evalm(SA/rowsum[1]):print(PP,QQ,ST);fi; od;od;od;od; |
| > |
J2:=IdentityMatrix(binomial(n,2)): |
| > |
for i1 in 1 do for i2 in 1,2 do for i3 in 1,2 do for i4 in 1,2 do ee:=[bit[i1],bit[i2],bit[i3],bit[i4]];phi:=diag(seq(ee[q],q=1..n)); Detta:=Matrix(multiply(phi,Delta));Rx:=evalm(A+Detta); Bx:=evalm(A-Detta); |
| > |
RR:=sympow(evalm(Rx),2):BB:=sympow(evalm(Bx),2);AA:=evalm((1/2)*(RR+BB)):LL:=map(limit,evalm((1-s)*inverse(JI-s*AA)),s=1);print(ee,iszero(LL),det(J2-AA)); |
![[1, 1, 1, 1], false, 0](images/RCC2OUT_116.gif)
![[1, 1, 1, -1], true, 1/4](images/RCC2OUT_117.gif)
![[1, 1, -1, 1], true, 1/4](images/RCC2OUT_118.gif)
![[1, 1, -1, -1], false, 0](images/RCC2OUT_119.gif)
![[1, -1, 1, 1], true, 1/4](images/RCC2OUT_120.gif)
![[1, -1, 1, -1], false, 0](images/RCC2OUT_121.gif)
![[1, -1, -1, 1], true, 1/4](images/RCC2OUT_122.gif)
![[1, -1, -1, -1], true, 1/4](images/RCC2OUT_123.gif)
![vector([-1, 1, 0, -1]), true](images/RCC2OUT_124.gif)
| > |
matrans(R);matrans(B);rank(A);"rank of Delta"=d;print(pi,evalm(pi/sigma)); |
![vector([4, 3, 1, 2])](images/RCC2OUT_125.gif)
![vector([3, 4, 4, 3])](images/RCC2OUT_126.gif)

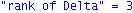
![vector([1, 1, 2, 2]), vector([1/6, 1/6, 1/3, 1/3])](images/RCC2OUT_129.gif)
| > |
############################ END FOURS ################################################## |
| > |
########################## RUNNING TWELVES ############################### |
| > |
#for i1 in 1 do for i2 in 1,2 do for i3 in 1,2 do for i4 in 1,2 do for i5 in 1,2 do for i6 in 1,2 do for i7 in 1,2 do for i8 in 1,2 do for i9 in 1,2 do for ia in 1,2 do for ib in 1,2 do for ic in 1,2 do ee:=[bit[i1],bit[i2],bit[i3],bit[i4],bit[i5],bit[i6],bit[i7],bit[i8],bit[i9],bit[ia],bit[ib],bit[ic]]; phi:=diag(seq(ee[q],q=1..n));unassign('Y');Y[1]:=multiply(pi,phi,Delta):for i from 2 to d do Y[i]:=map(simplify,multiply(Y[i-1],phi,Delta)) od:KK:=stackmatrix(seq(Y[b],b=1..d));eee:=evalm((1/2)*(ee+u));KU1:=ecliffe(map(expand,evalm(KK&*transpose(Delta))));NS1:=NullSpace(Matrix(KU1));for i to doDIM(NS1) do print(NS1[i],checkspan(ISX,NS1[i]),multiply(NS1[i],Delta)) od;print(eee,evalb(d=rank(KK)),"rank KU1 ",rank(KU1),"nullspace ", NS1) od;od;od;od;od;od;od;od;od;od;od;od; |
| > |
########################################################## |
| > |
d:=rank(Delta);matrans(R),matrans(B);## |
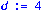
![vector([6, 1, 5, 6, 1, 5]), vector([2, 5, 1, 2, 3, 4])](images/RCC2OUT_131.gif)
| > |
omx:=vector(n,i->if i=1 then 1 else 0 fi); |
![omx := vector([1, 0, 0, 0, 0, 0])](images/RCC2OUT_132.gif)
| > |
for i1 in 1 do for i2 in 1,2 do for i3 in 1,2 do for i4 in 1,2 do for i5 in 1,2 do ee:=[bit[i1],bit[i2],bit[i3],bit[i4],bit[i5]];phi:=diag(seq(ee[q],q=1..n)); deta:=Matrix(multiply(phi,Delta)); print(ee,map(evalf,map(evalc,map(simplify,multiply(htranspose(F),deta,F)))));for i to d do print(i,map(evalf,map(evalc,map(simplify,multiply(htranspose(F),Omega,deta^i,F))))) od; od;od;od;od;od; |
| > |
deta:=factor(det(A+tau*phi&*Delta)); |
![deta := -1/8*tau*(-tau^2*e[1]*e[3]*e[4]+tau^2*e[2]*e[3]*e[4]-tau^2*e[1]*e[2]*e[4]+tau^2*e[1]*e[3]*e[2]+e[4]-e[3]-e[2]+e[1])](images/RCC2OUT_133.gif)
#for i1 in 1 do for i2 in 1,2 do for i3 in 1,2 do for i4 in 1,2 do ee:=[bit[i1],bit[i2],bit[i3],bit[i4]];x:=ecliffsubs(deta,ee);y:=subs(tau=1,x);z:=subs(tau=-1,x); print(ee," ",x,y,z) od;od;od;od;
| > |
########################################################################### |
| > |
################################### KERNEL ################################# |
| > |
########################################################################### |
| > |
#multiply(pir,B,R,R,B,B,B,R); |
| > |
unassign('IDEMS'):read "/home/ph/GAP/idems"; |
![IDEMS[1] := [[0, 0, 0, 0, 0, 1], [0, 0, 1, 0, 0, 0], [0, 0, 1, 0, 0, 0], [0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 1]]](images/RCC2OUT_134.gif)
![IDEMS[2] := [[0, 0, 0, 0, 1, 0], [0, 0, 0, 1, 0, 0], [0, 0, 0, 1, 0, 0], [0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 1, 0]]](images/RCC2OUT_135.gif)
![IDEMS[3] := [[0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 1, 0], [0, 0, 0, 1, 0, 0], [0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 1, 0], [0, 0, 0, 0, 1, 0]]](images/RCC2OUT_136.gif)
![IDEMS[4] := [[0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 1], [0, 0, 1, 0, 0, 0], [0, 0, 1, 0, 0, 0], [0, 0, 0, 0, 0, 1], [0, 0, 0, 0, 0, 1]]](images/RCC2OUT_137.gif)
![IDEMS[5] := [[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [1, 0, 0, 0, 0, 0], [1, 0, 0, 0, 0, 0]]](images/RCC2OUT_138.gif)
![IDEMS[6] := [[1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [1, 0, 0, 0, 0, 0], [1, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0]]](images/RCC2OUT_139.gif)
| > |
for i to doDIM(IDEMS) do matrans(IDEMS[i]) od; |
![vector([6, 3, 3, 3, 6, 6])](images/RCC2OUT_140.gif)
![vector([5, 4, 4, 4, 5, 5])](images/RCC2OUT_141.gif)
![vector([4, 5, 4, 4, 5, 5])](images/RCC2OUT_142.gif)
![vector([3, 6, 3, 3, 6, 6])](images/RCC2OUT_143.gif)
![vector([1, 2, 2, 2, 1, 1])](images/RCC2OUT_144.gif)
![vector([1, 2, 1, 1, 2, 2])](images/RCC2OUT_145.gif)
| > |
C:=choose(n,2):print(seq({i,C[i]},i=1..binomial(n,2))); |
![{1, [1, 2]}, {2, [1, 3]}, {3, [1, 4]}, {4, [1, 5]}, {5, [1, 6]}, {6, [2, 3]}, {7, [2, 4]}, {8, [2, 5]}, {9, [2, 6]}, {10, [3, 4]}, {11, [3, 5]}, {12, [3, 6]}, {13, [4, 5]}, {14, [4, 6]}, {15, [5, 6]}](images/RCC2OUT_146.gif)
![{1, [1, 2]}, {2, [1, 3]}, {3, [1, 4]}, {4, [1, 5]}, {5, [1, 6]}, {6, [2, 3]}, {7, [2, 4]}, {8, [2, 5]}, {9, [2, 6]}, {10, [3, 4]}, {11, [3, 5]}, {12, [3, 6]}, {13, [4, 5]}, {14, [4, 6]}, {15, [5, 6]}](images/RCC2OUT_147.gif)
| > |
#for i to doDIM(IDEMS) do asym2(IDEMS[i]) od; |
| > |
#for i to doDIM(IDEMS) do KRISPS[i]:=multiply(Omega,IDEMS[i]):KROSPS[i]:=multiply(spi,IDEMS[i]):print(matrans(IDEMS[i]),KROSPS[i]) od: |
| > |
#KRSPS:=stackmatrix(seq(KROSPS[i],i=1..doDIM(IDEMS))):RS:=rowspace(KRSPS);for i to doDIM(RS) do VS[i]:=evalm(uu&*transpose(convert(RS[i],matrix))) od; |
| > |
#checkspan(VS,Omega),expVec(VS,Omega); |

| > |
#MK:=stackmatrix(seq(KROSPS[i],i=1..doDIM(IDEMS)));rank(MK); |
| > |
unassign('Q'):read "/home/ph/GAP/Q":for i to doDIM(Q) do matrans(evalm(Q[i])) od; |
![vector([4, 3, 4, 3])](images/RCC2OUT_149.gif)
![vector([4, 3, 3, 4])](images/RCC2OUT_150.gif)
![vector([3, 4, 4, 3])](images/RCC2OUT_151.gif)
![vector([3, 4, 3, 4])](images/RCC2OUT_152.gif)
![vector([2, 1, 2, 1])](images/RCC2OUT_153.gif)
![vector([2, 1, 1, 2])](images/RCC2OUT_154.gif)
![vector([1, 2, 2, 1])](images/RCC2OUT_155.gif)
![vector([1, 2, 1, 2])](images/RCC2OUT_156.gif)
| > |
#unassign('KBAS'):read "/home/ph/GAP/kbas":for i to doDIM(KBAS) do evalm(KBAS[i]) od; |
| > |
#for i to doDIM(Q) do extpow(Q[i],2) od; |
| > |
#for i to doDIM(IDEMS) do checkspan(KBAS,IDEMS[i]);expVec(KBAS,IDEMS[i]) od; |
![matrix([[0, 0, 1/2, 1/2], [0, 0, 1/2, 1/2], [0, 0, 1/2, 1/2], [0, 0, 1/2, 1/2]])](images/RCC2OUT_157.gif)
| > |
XA:=matrix(2,2,[1,2,3,4]); |
![XA := matrix([[1, 2], [3, 4]])](images/RCC2OUT_158.gif)
| > |
map(convert,graycode(3),binary); |
![[0, 1, 11, 10, 110, 111, 101, 100]](images/RCC2OUT_159.gif)
| > |
det(J-t*A);det(J2-t*AA);det(J2-AA); |
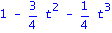
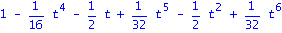

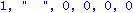
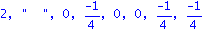
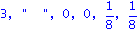

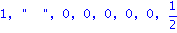
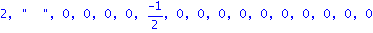
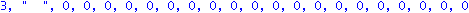
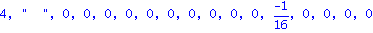
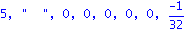
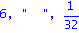
| > |
S2:=sympow(RR,2):for i to n do print(row(S2,i)) od;T2:=sympow(BB,2): |
![vector([0, 0, 0, 0, 0, 1/2+1/2*e[2]*e[1]])](images/RCC2OUT_173.gif)
![vector([0, -1/4*(e[1]-1)*(e[3]+1), 1/4*(e[1]+1)*(e[3]+1), 0, 0, 1/4*(e[1]-1)*(e[3]-1)])](images/RCC2OUT_174.gif)
![vector([0, 0, 0, -1/4*(e[1]-1)*(e[4]+1), 1/4*(e[1]+1)*(e[4]+1), -1/4*(e[1]+1)*(e[4]-1)])](images/RCC2OUT_175.gif)
![vector([0, 1/4*(e[2]+1)*(e[3]+1), -1/4*(e[2]-1)*(e[3]+1), 0, 0, -1/4*(e[2]+1)*(e[3]-1)])](images/RCC2OUT_176.gif)
| > |
D2:=evalm(S2-T2):A2:=evalm(S2+T2); |
![A2 := matrix([[0, 0, 0, 0, 0, 1+e[2]*e[1]], [0, -1/4*(e[1]-1)*(e[3]+1)-1/4*(e[1]+1)*(e[3]-1), 1/4*(e[1]+1)*(e[3]+1)+1/4*(e[1]-1)*(e[3]-1), 0, 0, 1/4*(e[1]+1)*(e[3]+1)+1/4*(e[1]-1)*(e[3]-1)], [0, 0, 0,...](images/RCC2OUT_177.gif)
![A2 := matrix([[0, 0, 0, 0, 0, 1+e[2]*e[1]], [0, -1/4*(e[1]-1)*(e[3]+1)-1/4*(e[1]+1)*(e[3]-1), 1/4*(e[1]+1)*(e[3]+1)+1/4*(e[1]-1)*(e[3]-1), 0, 0, 1/4*(e[1]+1)*(e[3]+1)+1/4*(e[1]-1)*(e[3]-1)], [0, 0, 0,...](images/RCC2OUT_178.gif)
![A2 := matrix([[0, 0, 0, 0, 0, 1+e[2]*e[1]], [0, -1/4*(e[1]-1)*(e[3]+1)-1/4*(e[1]+1)*(e[3]-1), 1/4*(e[1]+1)*(e[3]+1)+1/4*(e[1]-1)*(e[3]-1), 0, 0, 1/4*(e[1]+1)*(e[3]+1)+1/4*(e[1]-1)*(e[3]-1)], [0, 0, 0,...](images/RCC2OUT_179.gif)
![A2 := matrix([[0, 0, 0, 0, 0, 1+e[2]*e[1]], [0, -1/4*(e[1]-1)*(e[3]+1)-1/4*(e[1]+1)*(e[3]-1), 1/4*(e[1]+1)*(e[3]+1)+1/4*(e[1]-1)*(e[3]-1), 0, 0, 1/4*(e[1]+1)*(e[3]+1)+1/4*(e[1]-1)*(e[3]-1)], [0, 0, 0,...](images/RCC2OUT_180.gif)
![A2 := matrix([[0, 0, 0, 0, 0, 1+e[2]*e[1]], [0, -1/4*(e[1]-1)*(e[3]+1)-1/4*(e[1]+1)*(e[3]-1), 1/4*(e[1]+1)*(e[3]+1)+1/4*(e[1]-1)*(e[3]-1), 0, 0, 1/4*(e[1]+1)*(e[3]+1)+1/4*(e[1]-1)*(e[3]-1)], [0, 0, 0,...](images/RCC2OUT_181.gif)
![A2 := matrix([[0, 0, 0, 0, 0, 1+e[2]*e[1]], [0, -1/4*(e[1]-1)*(e[3]+1)-1/4*(e[1]+1)*(e[3]-1), 1/4*(e[1]+1)*(e[3]+1)+1/4*(e[1]-1)*(e[3]-1), 0, 0, 1/4*(e[1]+1)*(e[3]+1)+1/4*(e[1]-1)*(e[3]-1)], [0, 0, 0,...](images/RCC2OUT_182.gif)
![A2 := matrix([[0, 0, 0, 0, 0, 1+e[2]*e[1]], [0, -1/4*(e[1]-1)*(e[3]+1)-1/4*(e[1]+1)*(e[3]-1), 1/4*(e[1]+1)*(e[3]+1)+1/4*(e[1]-1)*(e[3]-1), 0, 0, 1/4*(e[1]+1)*(e[3]+1)+1/4*(e[1]-1)*(e[3]-1)], [0, 0, 0,...](images/RCC2OUT_183.gif)
| > |
ecliffe(simplify(det(J2-A2/2))); |
![-3/32*e[3]*e[4]*e[2]*e[1]+5/32-1/32*e[3]*e[1]-1/32*e[4]*e[2]-1/32*e[4]*e[3]-1/32*e[2]*e[1]+1/32*e[4]*e[1]+1/32*e[3]*e[2]](images/RCC2OUT_184.gif)
| > |
M:=matrix(2,2,[x,y,x*y,y*z]);dd:=det(M); |
![M := matrix([[x, y], [x*y, y*z]])](images/RCC2OUT_185.gif)
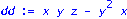
| > |
#for i to 8 do print(e[i]) od; |
| > |
unassign('a','b','c','d','e','f','g','h','i','p','q'): |

| > |
extpow(matrix(3,3,[a,b,c,d,e,f,g,h,i]),2); |
![matrix([[a*e-b*d, a*f-c*d, b*f-c*e], [a*h-b*g, a*i-c*g, b*i-c*h], [d*h-e*g, d*i-f*g, e*i-f*h]])](images/RCC2OUT_188.gif)
| > |
kron(evalm(UnitVector(3,5)),evalm(UnitVector(2,5))); |
Error, (in linalg:-rowdim) expecting a matrix
![matrix([[-2, 0, 0, 0, 0, 1+tau*e[1]*e[2]], [0, -3/2-1/2*tau*e[1]*e[3], 1/2+1/2*tau*e[1]*e[3], 0, 0, 1/2+1/2*tau*e[1]*e[3]], [0, 0, -2, 1/2-1/2*tau*e[1]*e[4], 1/2+1/2*tau*e[1]*e[4], 1/2-1/2*tau*e[1]*e[...](images/RCC2OUT_189.gif)
| > |
read "/home/ph/maple/cartan.txt"; |
Warning, the names GramSchmidt and fibonacci have been rebound
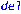


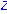










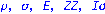
![matrix([[0, 0, 0, 0], [0, 0, 0, 1], [0, 0, 0, 0], [0, 1, 0, 0]])](images/RCC2OUT_210.gif)
| > |
v:=vector(binomial(n,2));w:=matrix(n,n,0): |
![v := array(1 .. 6, [])](images/RCC2OUT_211.gif)
| > |
k:=1:for i from 1 to n do for j from i+1 to n do if(i<>j) then w:=evalm(w+v[k]*sigma[i,j]) fi ;k:=k+1 od ;od; |
![matrix([[0, v[1], v[2], v[3]], [v[1], 0, v[4], v[5]], [v[2], v[4], 0, v[6]], [v[3], v[5], v[6], 0]])](images/RCC2OUT_212.gif)
| > |
r2:=sympow(R,2):b2:=sympow(B,2):cc:=matrix(n,n,(i,j)->if (j=1) then 1 else 0 fi):c2:=asym2(cc); |
![c2 := matrix([[0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0]])](images/RCC2OUT_213.gif)
| > |
v1:=evalm(extpow(phi,2)&*v); |
![v1 := vector([e[1]*e[2]*v[1], e[1]*e[3]*v[2], e[1]*e[4]*v[3], e[2]*e[3]*v[4], e[2]*e[4]*v[5], e[3]*e[4]*v[6]])](images/RCC2OUT_214.gif)
| > |
ww:=subs([seq(v[k]=r1[k],k=1..binomial(n,2))],evalm(w)); |
![ww := matrix([[0, 1/3, 2/9, 1/9], [1/3, 0, 1/9, 2/9], [2/9, 1/9, 0, 1/3], [1/9, 2/9, 1/3, 0]])](images/RCC2OUT_215.gif)
| > |
evalm(Omega&*ww&*Omega); |
![matrix([[1/9, 1/9, 2/9, 2/9], [1/9, 1/9, 2/9, 2/9], [1/9, 1/9, 2/9, 2/9], [1/9, 1/9, 2/9, 2/9]])](images/RCC2OUT_216.gif)
| > |
ecliffe(evalm(symult(A,w)+symult(Delta,w))); |
![matrix([[0, v[6], 1/2*v[3]+1/2*v[6], 1/2*v[5]], [v[6], 0, 1/2*v[2], 1/2*v[4]+1/2*v[6]], [1/2*v[3]+1/2*v[6], 1/2*v[2], 0, 1/2*v[1]+1/2*v[6]], [1/2*v[5], 1/2*v[4]+1/2*v[6], 1/2*v[1]+1/2*v[6], 0]])](images/RCC2OUT_217.gif)
| > |
evalm((1/2)*(symult(R,ww)+symult(B,ww))),evalm(ww); |
![matrix([[0, 1/3, 2/9, 1/9], [1/3, 0, 1/9, 2/9], [2/9, 1/9, 0, 1/3], [1/9, 2/9, 1/3, 0]]), matrix([[0, 1/3, 2/9, 1/9], [1/3, 0, 1/9, 2/9], [2/9, 1/9, 0, 1/3], [1/9, 2/9, 1/3, 0]])](images/RCC2OUT_218.gif)
| > |
print(ww);ev:=JordanForm(Matrix(ww),output=['J','Q']);pp:=ev[1]:U:=ev[2]: |
![matrix([[0, 1/3, 2/9, 1/9], [1/3, 0, 1/9, 2/9], [2/9, 1/9, 0, 1/3], [1/9, 2/9, 1/3, 0]])](images/RCC2OUT_219.gif)
![ev := Matrix([[0, 0, 0, 0], [0, 2/3, 0, 0], [0, 0, (-4)/9, 0], [0, 0, 0, (-2)/9]]), Matrix([[1/4, 1/4, 1/4, 1/4], [1/4, 1/4, (-1)/4, (-1)/4], [(-1)/4, 1/4, (-1)/4, 1/4], [(-1)/4, 1/4, 1/4, (-1)/4]])](images/RCC2OUT_220.gif)
| > |
evalm(transpose(2*U)&*(2*U)); |
![matrix([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]])](images/RCC2OUT_221.gif)
| > |
aa:=ecliffsubsmat(evalm(2*J2+aj),[1,1,1,1]); |
![aa := matrix([[0, 0, 0, 0, 0, 2], [0, 0, 1, 0, 0, 1], [0, 0, 0, 0, 1, 0], [0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 1], [1, 0, 0, 0, 0, 1]])](images/RCC2OUT_222.gif)
| > |
A2:=(ecliffsubsmat(evalm(aj/2+J2),[1,1,1,1])); |
![A2 := matrix([[0, 0, 0, 0, 0, 1], [0, 0, 1/2, 0, 0, 1/2], [0, 0, 0, 0, 1/2, 0], [0, 1/2, 0, 0, 0, 0], [0, 0, 0, 1/2, 0, 1/2], [1/2, 0, 0, 0, 0, 1/2]])](images/RCC2OUT_223.gif)
| > |
XX:=abel(A2);r1:=col(XX,1); |
![XX := matrix([[1/3, 0, 0, 0, 0, 2/3], [2/9, 0, 0, 0, 0, 4/9], [1/9, 0, 0, 0, 0, 2/9], [1/9, 0, 0, 0, 0, 2/9], [2/9, 0, 0, 0, 0, 4/9], [1/3, 0, 0, 0, 0, 2/3]])](images/RCC2OUT_224.gif)
![r1 := vector([1/3, 2/9, 1/9, 1/9, 2/9, 1/3])](images/RCC2OUT_225.gif)
![matrix([[0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0]])](images/RCC2OUT_226.gif)
| > |
ecliffit(multiply(pi,evalm(symult(phi&*Delta,w)),u)); |
![-e[3]*e[4]*v[5]+3/4*e[4]*v[4]*e[2]+3/4*e[2]*v[6]*e[4]+e[3]*e[4]*v[1]-3/4*e[1]*v[6]*e[4]+e[3]*e[4]*v[6]+3/4*e[1]*e[4]*v[5]-e[3]*e[4]*v[2]-3/4*e[4]*v[4]*e[1]-3/4*e[2]*e[4]*v[5]-3/4*e[2]*v[6]*e[3]-3/4*e[...](images/RCC2OUT_227.gif)
![-e[3]*e[4]*v[5]+3/4*e[4]*v[4]*e[2]+3/4*e[2]*v[6]*e[4]+e[3]*e[4]*v[1]-3/4*e[1]*v[6]*e[4]+e[3]*e[4]*v[6]+3/4*e[1]*e[4]*v[5]-e[3]*e[4]*v[2]-3/4*e[4]*v[4]*e[1]-3/4*e[2]*e[4]*v[5]-3/4*e[2]*v[6]*e[3]-3/4*e[...](images/RCC2OUT_228.gif)
| > |
evalm(symult(AT,pp)+symult(DT,pp)),print(pp); |
![Matrix([[0, 0, 0, 0], [0, 2/3, 0, 0], [0, 0, (-4)/9, 0], [0, 0, 0, (-2)/9]])](images/RCC2OUT_229.gif)
![matrix([[0, 0, 0, 0], [0, 2/3, 0, 0], [0, 0, (-4)/9, 0], [0, 0, 0, (-2)/9]])](images/RCC2OUT_230.gif)
| > |
AT:=multiply(transpose(U),4*A,U);DT:=symmult(U,4*Delta);OT:=symmult(U,4*Omega); |
![AT := matrix([[(-1)/2, 0, 0, 0], [(-1)/2, 1, 0, 0], [0, 0, (-1)/2, 0], [0, 0, 1/2, 0]])](images/RCC2OUT_231.gif)
![DT := matrix([[(-1)/2, 0, 0, 0], [1/2, 0, 0, 0], [0, 0, 1/2, -1], [0, 0, 1/2, 0]])](images/RCC2OUT_232.gif)
![OT := matrix([[0, 0, 0, 0], [(-1)/3, 1, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]])](images/RCC2OUT_233.gif)
| > |
symult(B,phi);matrans(B); |
![matrix([[e[3], 0, 0, e[3]], [0, e[4], e[4], 0], [0, e[4], e[4], 0], [e[3], 0, 0, e[3]]])](images/RCC2OUT_234.gif)
![vector([3, 4, 4, 3])](images/RCC2OUT_235.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![matrix([[0, 0, -1, 1], [0, 0, 1, -1], [1, 0, 0, -1], [0, 1, -1, 0]])](images/RCC2OUT_11.gif)
![]()
![matrix([[85/512, 85/512, 171/512, 171/512], [85/512, 85/512, 171/512, 171/512], [43/256, 85/512, 85/256, 171/512], [85/512, 43/256, 171/512, 85/256]]), 0](images/RCC2OUT_13.gif)
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![aj := matrix([[-2, 0, 0, 0, 0, 1+e[1]*e[2]], [0, -3/2-1/2*e[1]*e[3], 1/2+1/2*e[1]*e[3], 0, 0, 1/2+1/2*e[1]*e[3]], [0, 0, -2, 1/2-1/2*e[1]*e[4], 1/2+1/2*e[1]*e[4], 1/2-1/2*e[1]*e[4]], [0, 1/2+1/2*e[2]*...](images/RCC2OUT_27.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![matrix([[10/9, 4/9, 11/18, 19/36], [4/9, 5/18, 7/36, 17/72], [11/18, 7/36, 13/36, 5/18], [19/36, 17/72, 5/18, 37/144]])](images/RCC2OUT_40.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![KK := matrix([[10/9, 4/9, 11/18, 19/36], [4/9, 5/18, 7/36, 17/72], [11/18, 7/36, 13/36, 5/18], [19/36, 17/72, 5/18, 37/144]])](images/RCC2OUT_53.gif)
](images/RCC2OUT_54.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![matrix([[0, 0, 1, 0], [0, 0, 0, 1], [0, 1, 0, 0], [1, 0, 0, 0]]), matrix([[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]])](images/RCC2OUT_67.gif)
![]()
![]()
![AA := matrix([[0, 0, 1/2, 0], [0, 0, 0, 1/2], [0, 1/2, 0, 0], [1/2, 0, 0, 0]])](images/RCC2OUT_70.gif)
![matrix([[0, 0, 0, 0], [0, 0, 0, 0], [1/8, 1/8, 1/8, 1/8], [1/8, 1/8, 1/8, 1/8]])](images/RCC2OUT_71.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![matrix([[1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 0, 1/3, 0, 1/3, 1/6], [1/3, 1/12, 1/4, 1/4, 1/12, 0], [1/6, 7/24, 1/24, 1/8, 5/24, 1/6]]), 4,](images/RCC2OUT_83.gif)
![matrix([[1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 1/3, 0, 1/3, 0, 1/6], [0, 1/4, 1/12, 1/12, 1/4, 1/3], [1/6, 1/24, 7/24, 5/24, 1/8, 1/6]]), 4,](images/RCC2OUT_84.gif)
![matrix([[0, (-1)/6, 1/6, (-1)/6, 1/6, 0], [1/6, (-1)/12, 1/12, 1/12, (-1)/12, (-1)/6], [0, 1/8, (-1)/8, (-1)/24, 1/24, 0]])](images/RCC2OUT_85.gif)
![]()
![]()
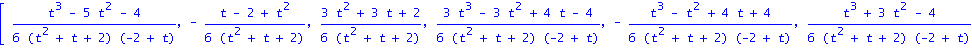

![]()
![sys := {psi[0] = 1, psi[1] = -t*(t^2+4)/(-4-t^2+t^3), psi[3] = -4*t^3/(-4-t^2+t^3), psi[2] = -4*t^2/(-4-t^2+t^3)}](images/RCC2OUT_91.gif)
![KK := matrix([[0, (-1)/6, 1/6, (-1)/6, 1/6, 0], [1/6, (-1)/12, 1/12, 1/12, (-1)/12, (-1)/6], [0, 1/8, (-1)/8, (-1)/24, 1/24, 0]])](images/RCC2OUT_92.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![matrix([[0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0]]), matrix([[1/4, 1/4, 1/4, 1/4, 1/4, 1/4], [1/4, 1/4, 1/4, 1/4, 1/4, 1/4]...](images/RCC2OUT_102.gif)
![matrix([[0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0]]), matrix([[1/4, 1/4, 1/4, 1/4, 1/4, 1/4], [1/4, 1/4, 1/4, 1/4, 1/4, 1/4]...](images/RCC2OUT_103.gif)
![matrix([[1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 1/6, 1/6, 1/6, 1/6, 1/6], [1/6, 1/6, 1/6, 1/6, 1/6, 1/6]])...](images/RCC2OUT_104.gif)

![]()
![]()
![]()
![Matrix([[-.8880, .2950, .4813, 2.043], [.3157, .6855, -1.769, 1.102], [.4347, -2.196, -0.3228e-1, 1.074], [1., 1., 1., 1.]])](images/RCC2OUT_109.gif)
![]()
![]()
![]()
![]()
![]()
![matrix([[-.1954395076, -.5116672736, -.8278950396, .1207882584], [-.5116672736, -.1954395076, .1207882584, -.8278950396], [.8278950396, -.1207882584, -.1954395076, -.5116672736], [.1207882584, -.82789...](images/RCC2OUT_115.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![matrix([[0, 0, 1/2, 1/2], [0, 0, 1/2, 1/2], [0, 0, 1/2, 1/2], [0, 0, 1/2, 1/2]])](images/RCC2OUT_157.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![matrix([[a*e-b*d, a*f-c*d, b*f-c*e], [a*h-b*g, a*i-c*g, b*i-c*h], [d*h-e*g, d*i-f*g, e*i-f*h]])](images/RCC2OUT_188.gif)
![matrix([[-2, 0, 0, 0, 0, 1+tau*e[1]*e[2]], [0, -3/2-1/2*tau*e[1]*e[3], 1/2+1/2*tau*e[1]*e[3], 0, 0, 1/2+1/2*tau*e[1]*e[3]], [0, 0, -2, 1/2-1/2*tau*e[1]*e[4], 1/2+1/2*tau*e[1]*e[4], 1/2-1/2*tau*e[1]*e[...](images/RCC2OUT_189.gif)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![matrix([[0, 0, 0, 0], [0, 0, 0, 1], [0, 0, 0, 0], [0, 1, 0, 0]])](images/RCC2OUT_210.gif)
![]()
![matrix([[0, v[1], v[2], v[3]], [v[1], 0, v[4], v[5]], [v[2], v[4], 0, v[6]], [v[3], v[5], v[6], 0]])](images/RCC2OUT_212.gif)
![c2 := matrix([[0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0]])](images/RCC2OUT_213.gif)
![]()
![ww := matrix([[0, 1/3, 2/9, 1/9], [1/3, 0, 1/9, 2/9], [2/9, 1/9, 0, 1/3], [1/9, 2/9, 1/3, 0]])](images/RCC2OUT_215.gif)
![matrix([[1/9, 1/9, 2/9, 2/9], [1/9, 1/9, 2/9, 2/9], [1/9, 1/9, 2/9, 2/9], [1/9, 1/9, 2/9, 2/9]])](images/RCC2OUT_216.gif)
![matrix([[0, v[6], 1/2*v[3]+1/2*v[6], 1/2*v[5]], [v[6], 0, 1/2*v[2], 1/2*v[4]+1/2*v[6]], [1/2*v[3]+1/2*v[6], 1/2*v[2], 0, 1/2*v[1]+1/2*v[6]], [1/2*v[5], 1/2*v[4]+1/2*v[6], 1/2*v[1]+1/2*v[6], 0]])](images/RCC2OUT_217.gif)
![matrix([[0, 1/3, 2/9, 1/9], [1/3, 0, 1/9, 2/9], [2/9, 1/9, 0, 1/3], [1/9, 2/9, 1/3, 0]]), matrix([[0, 1/3, 2/9, 1/9], [1/3, 0, 1/9, 2/9], [2/9, 1/9, 0, 1/3], [1/9, 2/9, 1/3, 0]])](images/RCC2OUT_218.gif)
![matrix([[0, 1/3, 2/9, 1/9], [1/3, 0, 1/9, 2/9], [2/9, 1/9, 0, 1/3], [1/9, 2/9, 1/3, 0]])](images/RCC2OUT_219.gif)
![ev := Matrix([[0, 0, 0, 0], [0, 2/3, 0, 0], [0, 0, (-4)/9, 0], [0, 0, 0, (-2)/9]]), Matrix([[1/4, 1/4, 1/4, 1/4], [1/4, 1/4, (-1)/4, (-1)/4], [(-1)/4, 1/4, (-1)/4, 1/4], [(-1)/4, 1/4, 1/4, (-1)/4]])](images/RCC2OUT_220.gif)
![matrix([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]])](images/RCC2OUT_221.gif)
![aa := matrix([[0, 0, 0, 0, 0, 2], [0, 0, 1, 0, 0, 1], [0, 0, 0, 0, 1, 0], [0, 1, 0, 0, 0, 0], [0, 0, 0, 1, 0, 1], [1, 0, 0, 0, 0, 1]])](images/RCC2OUT_222.gif)
![A2 := matrix([[0, 0, 0, 0, 0, 1], [0, 0, 1/2, 0, 0, 1/2], [0, 0, 0, 0, 1/2, 0], [0, 1/2, 0, 0, 0, 0], [0, 0, 0, 1/2, 0, 1/2], [1/2, 0, 0, 0, 0, 1/2]])](images/RCC2OUT_223.gif)
![XX := matrix([[1/3, 0, 0, 0, 0, 2/3], [2/9, 0, 0, 0, 0, 4/9], [1/9, 0, 0, 0, 0, 2/9], [1/9, 0, 0, 0, 0, 2/9], [2/9, 0, 0, 0, 0, 4/9], [1/3, 0, 0, 0, 0, 2/3]])](images/RCC2OUT_224.gif)
![]()
![matrix([[0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0]])](images/RCC2OUT_226.gif)
![]()
![]()
![Matrix([[0, 0, 0, 0], [0, 2/3, 0, 0], [0, 0, (-4)/9, 0], [0, 0, 0, (-2)/9]])](images/RCC2OUT_229.gif)
![matrix([[0, 0, 0, 0], [0, 2/3, 0, 0], [0, 0, (-4)/9, 0], [0, 0, 0, (-2)/9]])](images/RCC2OUT_230.gif)
![AT := matrix([[(-1)/2, 0, 0, 0], [(-1)/2, 1, 0, 0], [0, 0, (-1)/2, 0], [0, 0, 1/2, 0]])](images/RCC2OUT_231.gif)
![DT := matrix([[(-1)/2, 0, 0, 0], [1/2, 0, 0, 0], [0, 0, 1/2, -1], [0, 0, 1/2, 0]])](images/RCC2OUT_232.gif)
![OT := matrix([[0, 0, 0, 0], [(-1)/3, 1, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]])](images/RCC2OUT_233.gif)
![matrix([[e[3], 0, 0, e[3]], [0, e[4], e[4], 0], [0, e[4], e[4], 0], [e[3], 0, 0, e[3]]])](images/RCC2OUT_234.gif)
![]()